Minimum Set Primers and Unique Probes Design Algorithms for
Differential Detection of Symptom-Related Pathogens
| HOME | |
| Introduction | |
| Methodology | |
| Tetra-Nucleotide Nucleation (TNN) | |
| Unique & Common Sections | |
| Nearest-Neighbor Model | |
| MCGA | |
| Linker Design | |
| Computational Results | |
| Bio-Experiment | |
| Conclusion | |
| Reference | |
In conventional PCR experiments, the amplification of one target sequence requires one pair of primers, one for forward and the other for reverse amplification. If n sequences are to be amplified simultaneously, 2n primers are required. The multiple-use primers can largely reduce the number of primers required. One primer may serve as forward and/or reverse primers for several sequences. For each sequence to be amplified, there must exist a primer pair that can serve as forward and reverse primer for the target sequence. We can transform the multiple-use primer design problem into a constrained set-covering problem (SCP). The minimum set of primer pairs must cover all target sequences. The constraints are defined so that for each sequence, there must exist at least one primer pair. The formulation of the constrained set covering problem is as follows:
subject to , such that
where n is the number of target sequences, aij is the element of n × l zero-one matrix, l is the number of primers, and k is index of primer pairs. If primer j is a primer (forward or reverse) for sequence i , aij = 1, otherwise aij = 0. If primer j is in the solution set, Xj = 1, otherwise Xj = 0. The set covering problem has been proved to be a NP-complete problem (Garey and Johnson, 1979) . Several heuristic approaches have been proposed for set covering problems. Here we used a genetic algorithm to solve the set covering problem in a reasonable amount of time. In the next section, we will describe the genetic algorithm we employed. |
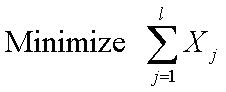 (6)
(6) 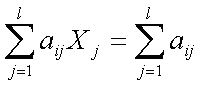 (7)
(7)