Java Programming


Location: Room 223B, 德田館
Time: 09:30 ~ 12:30

``Java is C++ without the guns, knives, and clubs.''
-- James Gosling

``Java is to JavaScript as ham is to hamster.''
-- Baruch Sadogursky

Course Information

Instructor Information

Wi-Fi Access

Grading Policy

You need to finish all programming labs as the minimal requirement to acquire the certificate of course completion. You could find your name here.

For the record, this course is offered without any course credit of National Taiwan University, in compliance with Implementation Regulations Governing Colleges Continuing Education, Ministry of Education.

Make-up Class Method Students are advised to utilize the website NTU COOL for class compensation. Please note, the required login credentials are those associated with your individual training class account.

Recording Classroom Lectures Policy Recording of classroom lectures is prohibited unless advance written permission is obtained from the class instructor and any guest presenter(s).

Goal

This course is designed for the students who want to learn Java but have no programming experience before. We will start with the very beginning of program design and fundamental concepts about programs and machines. You are expected to be capable to implement your idea in Java independently after 30 hours of lectures. Furthermore, I wish you could learn other programming languages without suffering from starting over.

The topics delivered in the following weeks are as follows:

In my humble wish, I am trying to show you more than Java itself, but a big picture of computer science.

Syllabus

Algorithm-Based Programming

Object-Oriented Programming

OOP Design Rules

Applications

Schedule
[ 247, 250, 251, 252, 253, 254, 255, 260, 261, 263, 265, 266, 268, 269, 271, 274, 275, 276, 277, 278, 280, 281, 281n, 282, 283, 284, 286, 289, 290, 291, 292, 293, 294, 295, 296, 297, 298, 299, 301, 304, 305, 306, 307, 308, 310, 311, 312, 313, 314, 315, 316, 318, 319, 320, 321, 322, 323, 325, 326, 328, 329, 330, 331, 335, 336, 337, 338, 340, 341, 342, 343, 344, 347, 348, 349, 353, 355, 359, 361, 365, 369, 371, 379, 381, 384, 386, 390, 394, 397, 400, 402, 405, 407, 411, 415 ]

Date
Summary
2024.8.12
2024.8.13
2024.8.14
  • Flow controls
    • Selections (branching): if-else if-else, switch-case-default, ?: operator
    • Digression: pseudorandom number generator (PRNG)
    • Repetitions: while loop, do-while loop, for loop
  • Homework 1
2024.8.15
2024.8.16
  • Data structures
    • Arrays: syntax & memory allocation
    • Data generation by PRNG
    • Descriptive statistics: max/min, location of max/min (argmax/argmin), sum
    • For-each loops
    • Cloning arrays: shallow copy or deep copy
    • Random permutation (shuffling)
    • Sorting algorithms: bubble sort, selection sort, insertion sort
    • Searching algorithms: linear search, binary search
    • More data structures: a glimpse on linked list
  • Homework 2
2024.8.19 (video)
  • Data structures (cont'd)
    • Higher-dimensional arrays feat. memory model
    • Upgraded array: ArrayList with a short introduction to generics
    • Case study: reversing arrays (an example for space complexity)
  • Methods and recursion
    • Method definition & implementation
    • Call stack & variable scope (again, explained with memory model)
    • Method overloading
    • Methods with variable-length arguments
    • The main method with its argument list
    • Recursive algorithms: factorial, sum, greatest common divisor (gcd), Fibonacci numbers
  • Homework 3
2024.8.20
  • Object-oriented programming
    • Class & object
    • Encapsulation: private fields and public methods
    • Constructors
    • The this operator
    • Instance / static members
    • Briefing design patterns (take the singleton pattern as example)
    • Garbage collection (GC)
    • UML: class diagram
2024.8.21
  • Object-oriented programming (cont'd)
    • HAS-A relationship (aggregation)
    • First IS-A relationship: class inheritance
    • Constructor chaining and the super operator
    • Method overriding
    • Subtype polymorphism: Liskov substitution principle
  • Homework 4
2024.8.22
  • Object-oriented programming (cont'd)
    • The instanceof operator
    • Abstract class / method
    • Final variable / method / class
    • Second IS-A relationship: interface inheritance
    • Case study: strategy pattern
    • Wrapper classes: Integer, Double, etc
    • Immutability: take String as an example; string pool
    • Enum type
    • Access controls: public, protect, package, private
    • Nested classes: inner class, anonymous class, static class
    • Case study: linked list, iterator pattern
2024.8.23
Promotion

Sample Code

Gradebook

Programming Labs

Late Homework Policy All programming labs should be submitted before the last date of class in order to deliver your final grades to the office so that the certificates can be issued soon. (See a recent complaint letter here.)

Homework Submission Send your source codes (the files with .java extension) to my email address shown in the beginning of this course page. Remember to indicate the class number, your full (Chinese) name, and homework number in the email title. For example, [Java 415] Homework 1 盧政良. Do not attach any class file because any executable file will be ruled out by Gmail.

Lab 0 Genesis

Install JDK22 and Eclipse (or any IDE you have been familiar with, say IntelliJ) in your computer (desktop/laptop). Note that you have to sign up an Oracle account before downloading the JDK installer. No need to email me for this lab unless you cannot complete the installation. You may also know the JDK binaries offered by different vendors, which are summarized in this article.

Lab 1 Number-Guessing Game

Write a program for number-guessing game (you may refer to Guess the Number if you have never played this game). The program first generates a secret number ranging between 0 and 99, inclusive. Then the program asks the player to guess a number. If the input number is equal to the secret number, then the player wins. If not, then update the range depending on the input accordingly. (For example, assume that the secret number is 42. If the player types 50 for the first time, then the program shows (0, 49) on the screen.) When there is only one integer left, the player loses the game. Also, make sure that the player types a number in the feasible range; otherwise, ask the player to redo the input.

Lab 1-1 (Optional)

Add some strategies (AI?) to play this game and calculate each winning rate by using these strategies for 1e5 times. For example, the naive strategy is to guess a number in random, and its result is around 66%. Surprisingly, the winning rate for binary search is about 63%, not as expected to beat the naive one. Why?

Lab 1-2 (Optional)

Find the optimal strategy to beat the former two. The result is shown below. As you could see, the winning rate of my optimal strategy reaches 99%!

Lab 1-3 (Optional)

Modify the game loop which allows the player to guess at most 7 times (why?). Also report their performance like below:

The performance of binary search remains ~63% while the other two degrade severely!

Lab 2 Contagion Control

The virus, COVID-19 (aka Wuhan coronavirus), is primarily spread from close contact with infected people. Your task is to design an algorithm to identify the chain of virus transmission from one person to the next. For simplicity, let N be the number of citizens, each denoted by an integer ID from 0 to N − 1. Each citizen is asked to keep a record of the ID of the person they comes in contact with. It is assumed that no two citizens keep the same ID of the citizen in close contact. To avoid typing numbers by hand, I suggust using the shuffling algorithm to generate a random sequence of 0, 1, 2, ..., N − 1 for testing. For example, consider N = 16 and assume that the citizen with ID 0 is initially infected. Your program is to identify and list all IDs along this infection chain. A possible output is shown below.

Lab 2-1 (Optional)

Modify your solution to show all group members and calculate how many groups in the random sequence. For example, consider N = 16 and the outputs are shown as follows.

Lab 2-2 (Optional)

Replace the native array by ArrayList. This lab asks you to understand the usage of ArrayList and Java generics, which won't be introduced comprehensively in this lecture (see Java Programming 2).

Lab 3 Performance Benchmark for Sorting Algorithms

First, implement three sorting algorithms (bubble sort, selection sort, and insertion sort) mentioned in class. Then compare the running time of these sorting algorithms together with Arrays.sort() (check its API here). Since the performance of these comparison-based sorting algorithms is sensitive to the order of data sequence, I suggest that you could calculate the average running time for various sizes and make a benchmark for these four algorithms (using the doubling hypothesis), shown as below.

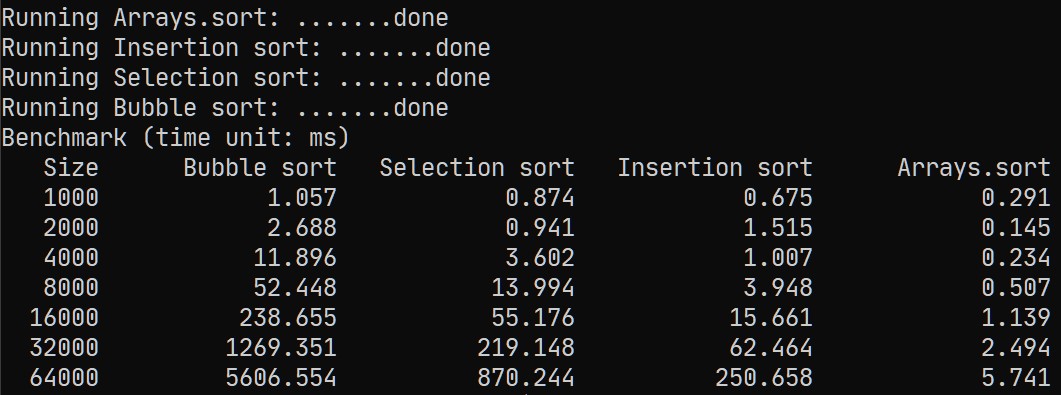
You may use System.currentTimeMillis() or System.nanoTime() to make timestamps (remember to use long variables). Note that the actual numbers in the table may differ from mine due by to variety of runtime environments. For your information, the benchmark test is completed on AMD Ryzen 9 3900X with the memory DDR4-3200 128 GB. If you are interested, you may watch this video for 15 sorting algorithms.

Lab 3-1 (Optional)

Compare the growth rate of running time for each sorting algorithm to the theoretical prediction by big-O. Recall that the first three sorting algorithms runs in O(n ^ 2) time while Arrays.sort() runs in O(n log n) time.

Lab 3-2 (Optional)

Implement the algorithm of cocktail sort which runs in O(n ^ 2) time. You may refer to cocktail sort in Wikipedia.

Lab 3-3 (Optional)

Implement Shell's sorting algorithm which runs in O(n (log n) ^ 2) time. You may refer to shell sort in Wikipedia, or this article.

Lab 3-4 (Optional)

Implement the merge sort algorithm which runs in O(n log n) time. You may refer to merge sort in Wikipedia.

Lab 3-5 (Optional)

Implement the quick sort algorithm which runs in Θ(n log n) time. You may refer to quick sort in Wikipedia.

Lab 4 Fast Power Using Recursion

Let x be any real number and n be any nonnegative integer. Write a program which calculates x ^ n by recursion. For example, 2 ^ 10 = 1024. Try to make your program run in O(log n) time. Note that you are not allowed to use Math.pow() and any loop in your solution.

Lab 4-1 (Optional)

Compare your solution to the naive method (running in O(n) time). Report the speedup.

Lab 4-2 (Optional)

As you can see, the double overflow occurs when the exp exceeds 1000. To calculate the correct numbers, you may use BigDecimal for arbitrary digits.

Lab 4-3 (Optional)

Modify your solution for negative n.

Lab 4-4 (Optional)

Convert the recursion version into the loop version.

Lab 4-5 (Optional)

Introduce bitwise operators (&) and shift operators (>>) to your solution.

Lab 4-6 (Optional)

Let M be any positive int value. Write a function to calculate x ^ n mod M for n = 10000000. You may use the polynomial remainder theorem (see here).

Lab 5 Refactoring Number-Guessing Game by Using Proper Design Patterns

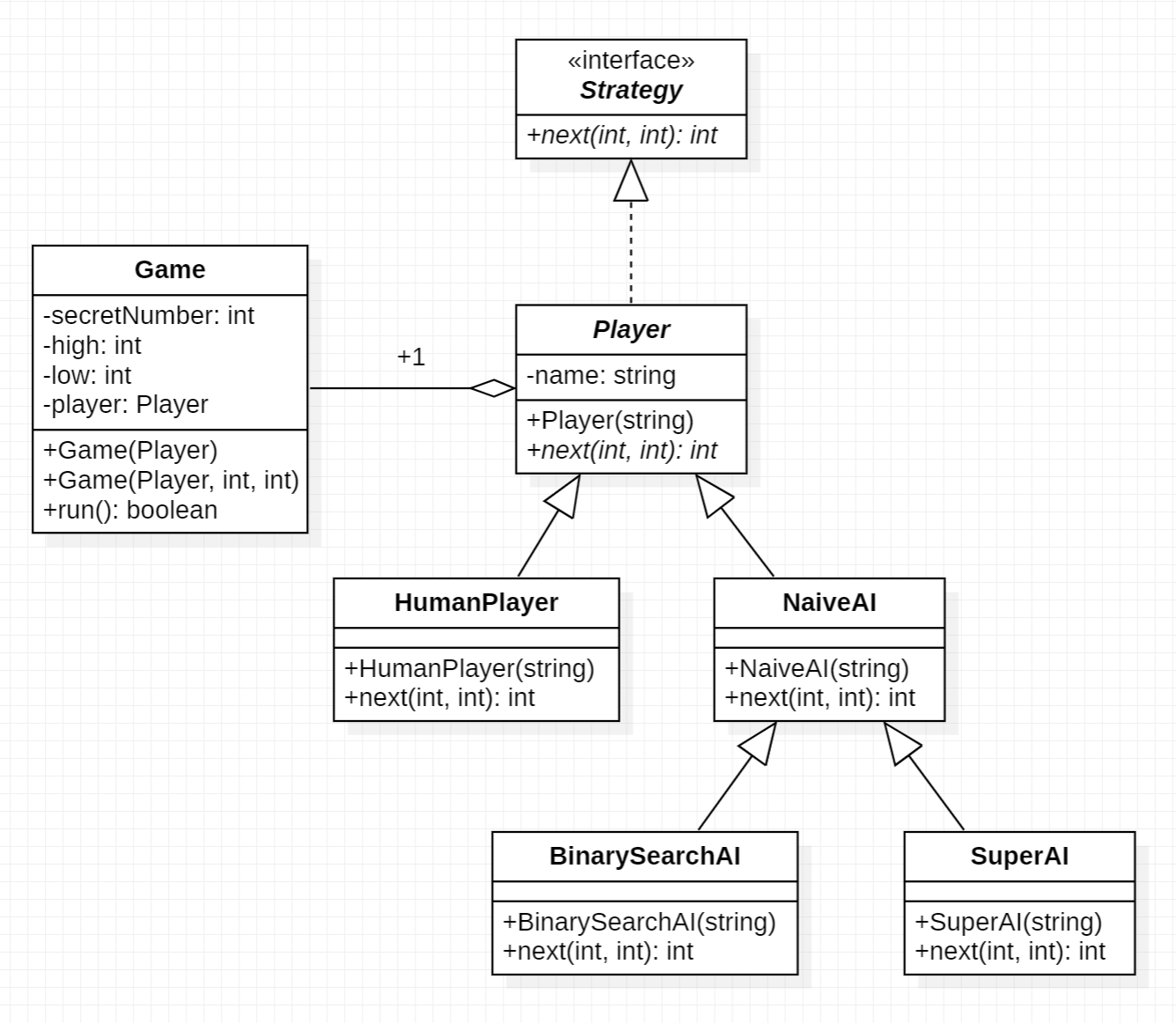
Rewrite your program of Lab 1 in OOP style. First analyze the functionalities of Lab 1 and then define at least two classes for each functionality. For instance, you could create two objects: one object to manage the game procedure, the other for the player who generates an integer within feasible range during the game. To achieve this, you will need to define a protocol, similar to the relationship between the System.out.println method and the toString method of any Java object. Hence the game will have minimal dependency on the player (the game won't need to know which kind of player during the game procudure). A possible class design in UML is shown below.

Lab 5-1 (Optional)

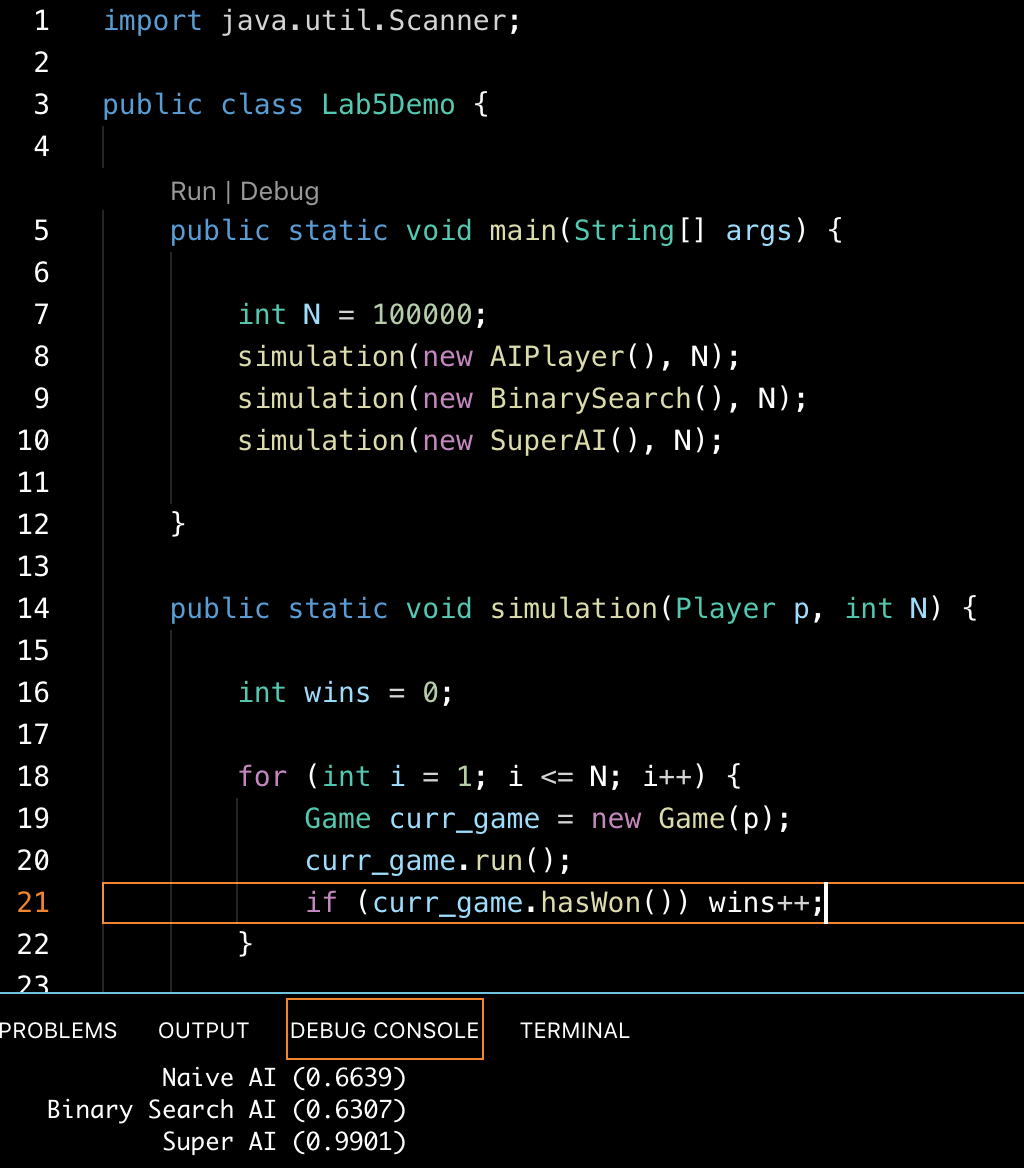
Try various strategies for this game. For example, the naive strategy is to guess a number in random, and the binary-search strategy is to return the number in the middle of the feasible range. Then compare the winning rates by simulating these strategies for 1e5 times.

Monte Carlo Labs

These labs listed below are not manditory.

Estimation of Euler Constant

Write a program which estimates the Euler constant e ~ 2.7183 by Monte Carlo simulation. The procedure is as follows: (1) Set N = 1e5 and M = 0; (2) for each iteration, find the minimal number k of random numbers which follows a standard uniform distribution (simply use Math.random() in this case) so that the sum of these random numbers is greater than 1; (3) do M += k; (4) then the estimator of e can be done by M / N.

Geometric Brownian Motion

Write a program which simulates the price movement of one stock by Monte Carlo simulation. The input is as follows: (1) S (spot price), (2) r (annual interest rate), (4) v (annual volatility), (5) T (time to maturity, year), (6) m (periods within T), (7) N (number of replicates). Now define dt = T/ m. For each time 0 < i <= m, calculate the future price S(i) by S(i) = S(i - 1) * exp((r − 0.5 * v ^ 2) * dt + v * sqrt(dt) * RANDN), where RANDN is a random variable following a standard normal distribution (use the method nextGaussian() of Random objects; see Random from Oracle). Repeat the procedure above for N times. Then draw all price paths on the canvas. You may refer to my solution: GBM.zip.

European Call Price

Write a program which calculates the price of European call options. The input is as follows: (1) S (spot price), (2) X (strike price), (3) T (time to maturity, year), (4) v (annual volatility), (5) r (annual interest rate), (6) N (sample size). The price of European call options can be done as follows: (1) Set N = 1e5 and the call price c = 0; (2) for each iteration, calculate the future price S’ by S’ = S * exp((r − 0.5 * v ^ 2) * T + v * sqrt(T) * RANDN), where RANDN is a random variable following a standard normal distribution (use the method nextGaussian() of Random objects; see Random from Oracle); (3) if S’ − X > 0, do c += S’ − X; (4) after N iterations, do c /= N. Finally, output the option price c. For example, the European call price is 14.2xxx for the case of S = 100, X = 100, T = 1, v = 0.3, r = 0.05.

References

Java (Introductory Level)

Java (Advanced Level)

Data Structures and Algorithms

Object-Oriented Analysis & Design

Computer Organization/Architecture

AP Computer Science

Taiwan

American School

Misc

Additional Reading