
¡@This page demo is based on : Cheng-Yuan
Liou, Quan-Ming Chang, "Active mesh for Minimal Surface Problems"
|| C 16
¡@The Mesh to emulate soap films is somewhere dramatically powerful than any
other complicated computational algorithms. This demo is going to show one
of its adventages by using the Mesh to solve the Minimal Surface Problem.
We are going to briefly introduce our model and training method, and take
the theory into practice.
¡@The Mesh is composed of many circles, each of which has four nodes. We call
a circle as a " Snack" and each one tries to minimum itself's energe
function,
¡@¡@¡@¡@¡@¡@¡@![]() .
.
¡@Therefore, the total energe function of the Mesh is¡@![]() , and it causes the shrinking and balancing to the Mesh.
, and it causes the shrinking and balancing to the Mesh.
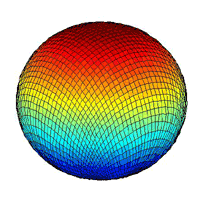
¡@The 2-D mesh put over a 3-D space should be molded at first for a convenient
handling. The method recommended here is to pull the Mesh to a virtual ball
and tie the border together, as the soap film we ever saw.
¡@ ¡@¡@¡@
¡@¡@¡@
¡@¡@¡@¡@Molding a 30x30 Mesh by pulling it to a virtual ball.¡@¡@¡@¡@¡@¡@¡@¡@¡@¡@
¡@¡@The result of binding the border together.
¡@Then it is declared that to solve the Minimal Surface Problem is extremely
close to the nature balance of the soap film Mesh if the weight inside its
energe function is well-designed. Here we are starting to set some examples
to interpret the idea:
¡@¡@¡@¡@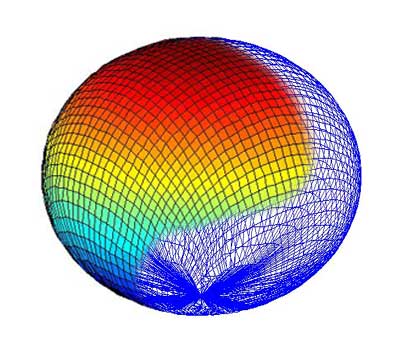 ¡@¡@
¡@¡@
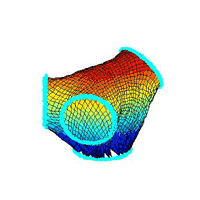
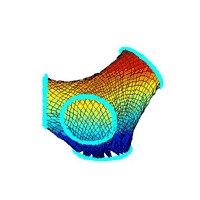
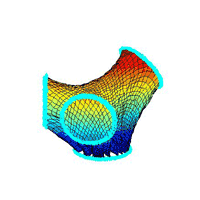
¡@The size of Mesh on this demo is 60x60, and the topography is made by T-shaped
pipes to hold tightly the nearby nodes, as above.
¡@![]()
¡@¡@¡@¡@¡@¡@¡@¡@¡@The Mesh demo
for Minimal Surface Problem
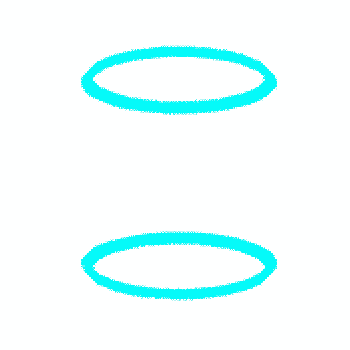 |
¡@moving flows
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
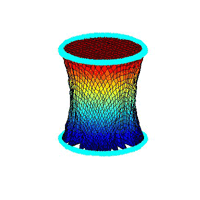 |
¡@result figures


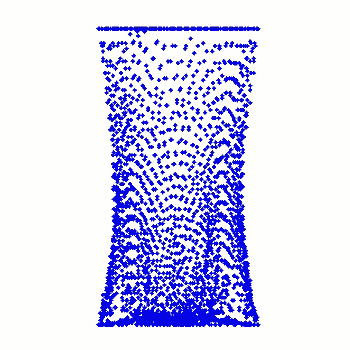

¡@topography 2:
 |
¡@moving flows
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
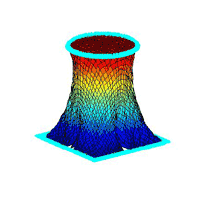 |
¡@result figures
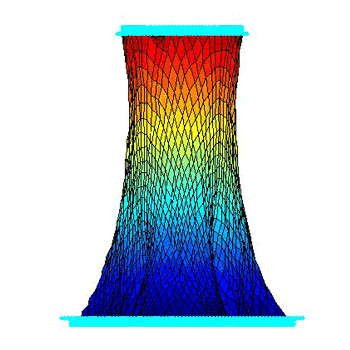

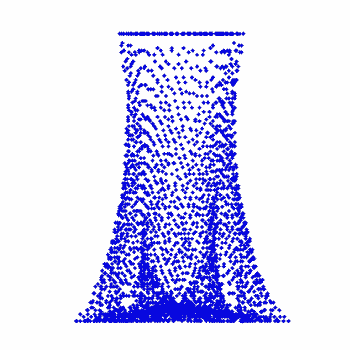

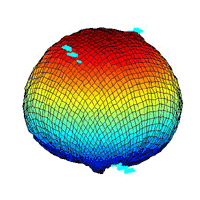
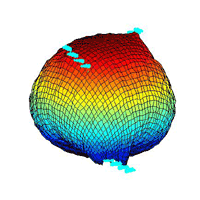
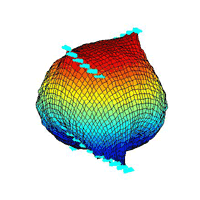
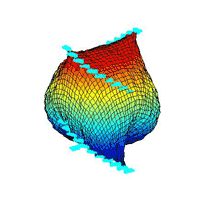
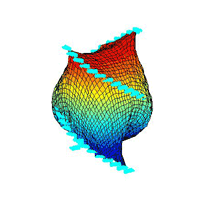
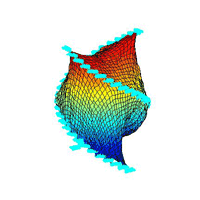
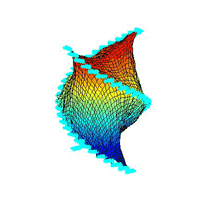
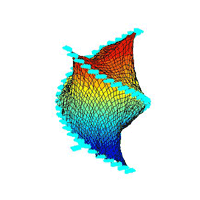
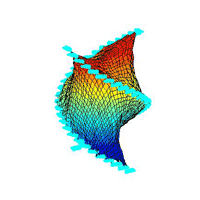
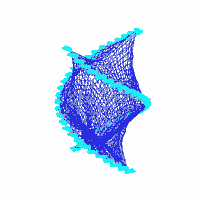
¡@topography 3:
 |
¡@moving flows
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
¡@result figures
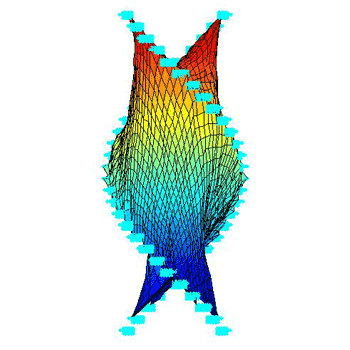
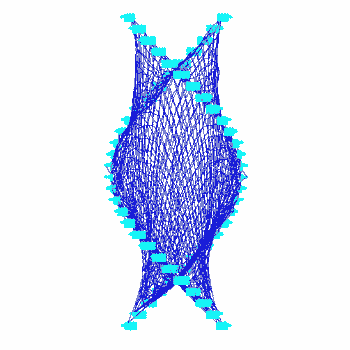


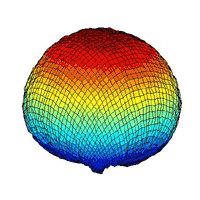
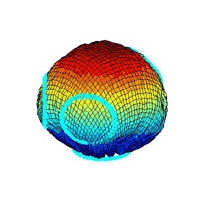
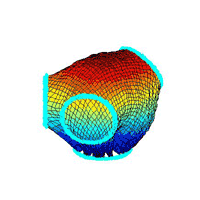
¡@topography 4:
 |
¡@moving flows
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
¡@result figures




¡@¡@For more detail and help, you can contact us: cyliou@csie.ntu.edu.tw .