(single source)  

Uneighted Graph :  Breath - First Search
Weighted Graph : Dijkstra's algorithm
 

        S {v₀};    for each v V do D[v]  d(v₀,v);                       *
        while  S  V do{
                  choose w S , D[w] min;
                  S S U {w};
                  for each v V-S  do                        *
                         D[v]  min(D[v] , D[w]+d[w,v]);
        }

Property :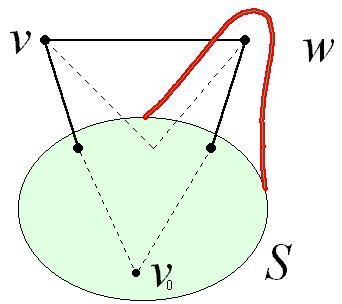

        v S  D[v] = shortest path from v₀ to v
        v S  D[v] = shortest path from v₀ to v through x (in S)
            proof : othewise , a path which is the combination of the path
                                               from v₀ to v and from v to w

Example

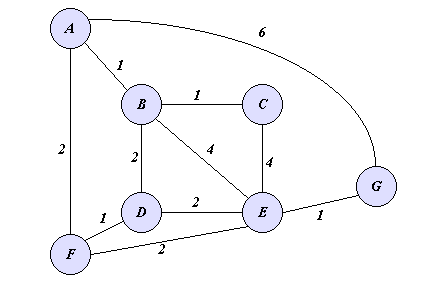
S	A	B	C	D	E	F	G
A	0	1				2	6
A   B	0	1	2	3	5	2	6
A   B   F	0	1	2	3	4	2	6
A   B   C    F	0	1	2	3	4	2	6
A   B   C    D   F	0	1	2	3	4	2	6
A   B   C    D   E   F	0	1	2	3	4	2	5
A   B   C    D   E   F   G	0	1	2	3	4	2	5

For both directed and undirected graph
 

T = O(N²)
 

Priority-First-Search implementation : Priority = D[w]+d(w , v)
 

Priority queue =  ; put(S);
 

Only modify D[v] , for w  v