Find Minimum Spanning Tree(for connected undirected graph)
            Tree : connected graph without cycle

                            u,v ,  a path from u to v.

            Spanning Tree : edges connect all vertice of G

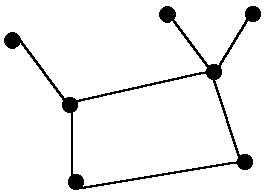
Lemma

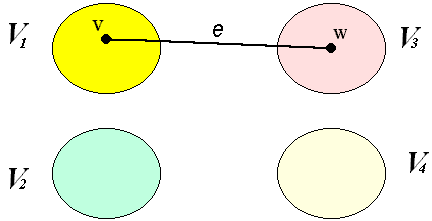
           V₁ V₂ V₃ V₄ = V
           e = (V,W) minimum edge,v V_i ,w V_i
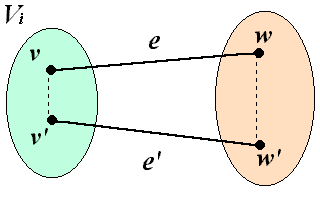
                 MST include e
           proof : (T - {e'}) e
                         is spanning tree of Lower cost.

Kruskal's algorithm
    vV , {v} a component;                                          W(e₁) W(e₂) .......W(e_N)
    repeat                                                                             for i = 1 to N do
            add minial edge across                                       if add e_i Not form cycle
                           2  components;                                                add e_{i
      Until  1  component remains}

Prim's algorithm
    V1 = visited

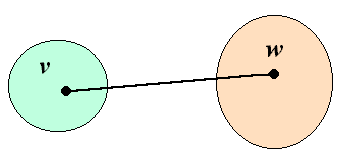
    V2 = unvisited

   e = (v , w)
      = minimal edge  visited vertex    fringe vertex
                                  

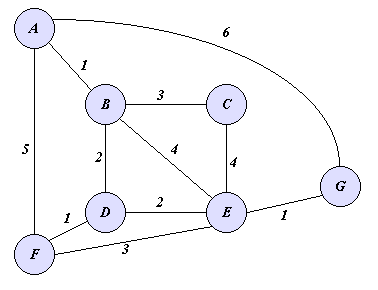
Priority - First - Search   implementation : Priority = Shortest length to tr