Voronoi Diagram
Given ai,
.., aN
-
Voronoi polygon (a) := all points closer to a than other aiˇs.
Verteices 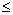 2N-4
2N-4
edges 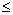 3N-6
3N-6
-
Voronoi diagram :=
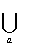 polygon(a)
polygon(a)
-
Voronoi Dual (Delaunay triangulation) triangulation of all points
-
Degree(vertx) = 3 (み)
Convex Hull 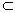 Dual
Dual
-
Polygon(a) unbounded
 a
a  convex
Hull
convex
Hull

Applications
-
closest pair find
closest pair of aiˇs
 (
(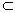 Dual)
Dual)
-
all nearest neighbor
find
nearest neighbor of ai (
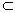 Dual)
Dual)
-
nearest neighbor find
nearest ai of a point P (P
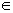 poly(ai))
poly(ai))
-
computing convex Hull
(
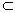 Dual)
Dual)
-
Euclidean Minimum Spanning
Tree (
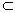 Dual)
Dual)
find a tree connects
all aiˇs with minimum distance.
-
Can compute Voronoi
Diagram in O(NlogN)
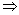 All can
be solved in O(NlogN)
All can
be solved in O(NlogN)
Compute Voronoi
Diagram in O(NlogN) time
(Divide & Conguer)

VD=( VD(L) 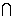 L(
L(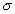 )
)
)
) 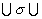 ( VD(R)
( VD(R) 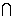 R(
R(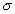 )
)
)
)
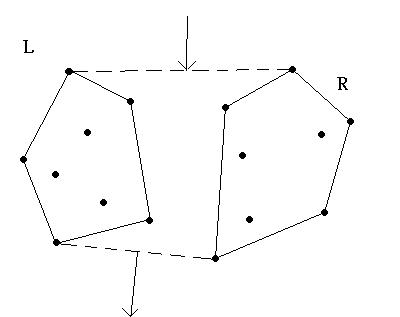
Compute Supporting Lines T=O(N)
-
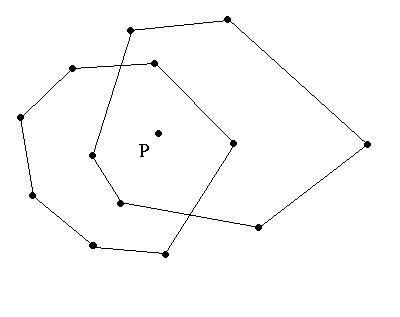
Compute CH(L)CH(R)
-
Find interior point
P of CH(L)
-
P interior point of
CH(R)
-
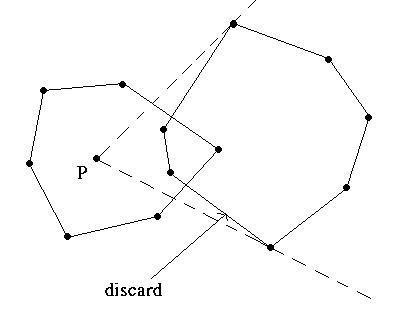
Merge CH(L)CH(R)
-
Graham Scan (NlogN
for convex Hull)
Property
Pinterior
point of CH  Angles of vertices of CH
Angles of vertices of CH 
![]() 3N-6
3N-6![]() 3N-6
3N-6
![]() L(
L(![]() )
)
)
) ![]() ( VD(R)
( VD(R) ![]() R(
R(![]() )
)
)
)
![]() Angles of vertices of CH
Angles of vertices of CH ![]()