alro

Network Flow

network：directed graph with ^S：source+capacity T：sink

flow f：exist dege e, 0≦f(e)≦c(e)

    exist vertex v≠s,t → Σf(i,v)=Σf(v,j)
                                          i            j

    value of f=|f|=Σf(i,t)=Σf(s,j)
                              i        j

Maximal flow problem：find the flow with max value

    cut(x,x)：x=v-x

      c(x→x)=Σc(v,w)：cut capacity
            v,w

    f(x→x)=Σf(v,w)：flow across the cut
            v,w

                                _
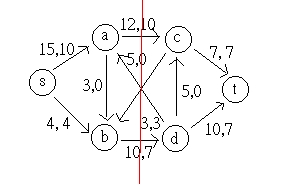
                         x      x          |f| = 14

      where v belongs to x, w belongs to x

    Lemma：|f|=f(x→x)-f(x→x)≦c(x→x)
    pf：|f|=|f|+0+0=Σout(v)-Σin(v)=f(x→x)-f(x→x)
                   s,a,b        s,a,b

Max-flow,min-cut Theorem (Ford,Fulkerson)

maxflow←→|f|=c(x,x)

augmenting path

         12,5    8,3    7,2                 c,f
        S—→a—→b—→t +5, —→f(e)<c(e)
               +7      +5     +5

               12,5   8,3     7,2                c,f
            S—→a—→b—→t   +3, ←—f(e)>0
           +7     -3      +5

Labelling algorithm：

find possible augmenting path, increase flow

example

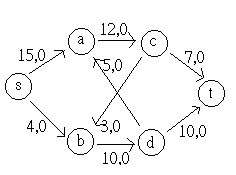4 10 5 12 7 s ----> c ----> d ----> a ----> b ----> t +4

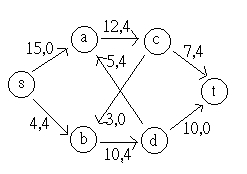15 8 3 6 10 s ----> a ----> b ----> c ----> d ----> t +3

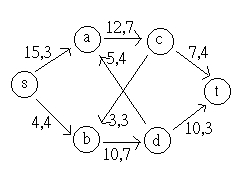12 5 3 s ----> a ----> b ----> t +4

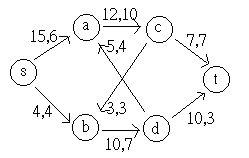9 -4 7 s ----> a ----> d ----> t +4

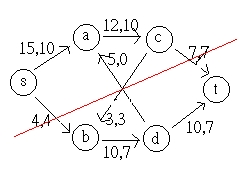F = 14

Drawbacks:

Irrational Capacity: might never terminate
Even Integral capacity: 2M increments

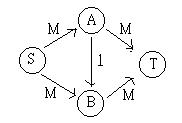
Edmond, Karp:

Breadth-First-Search + shortest path T = O(V³E)

Increase the Flow by Largest amount

priority-first-search implementation:

k->t size[k,t] >0 => priority = sizepk,t] - flow[k,t] k->t size[k,t] <0 => priority = -flow[k,t]

if priority < val[k] then priority = val[k];

val[k]=Max increase S→k

search stops when sink found;

Efficient in practice.