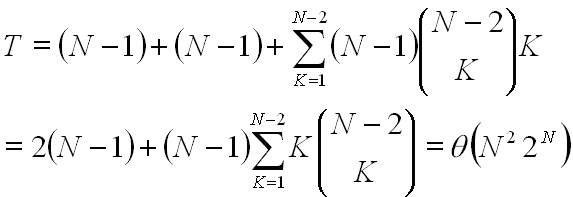Travelling dog
Find shortest simple path connects all nodes.
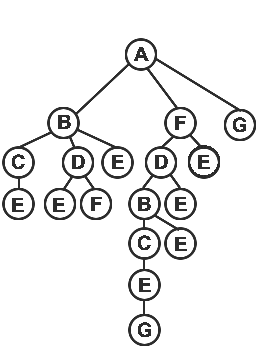
Exhaustive search + Prunning techniques: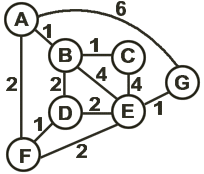
- Branch & Bound:
A F D B C E G = 11
A G E B = 11 already

- edge >= 1, 7 nodes totally
AG = 6

- Partial solution + MST >= 11

- Partial path + the rest nodes not connected (ABE)

- Others:
For Euclidean travelling salesman:
(graph distance = distance in plane)
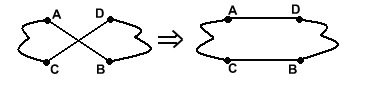 Generate permutation
generate N! permutations by exhaustively searching N-node complete graph
Generate permutation
generate N! permutations by exhaustively searching N-node complete graph
for K := 1 to N do val[K] := 0;
id := -1; Visit(0);
Visit(K)
id := id + 1; val[K] := id;
if id = V then writeperm;
for t := 1 to V do
if val[t] = 0 then Visit(t);
id := id - 1; val[k] := 0;
Travelling Salesman Problem
Find shortest simple cycle connects all nodes. (N! cycles)
Dynamic Programming
g(i, S) := shortest path i ---> 1 (thru nodes in S only)
- TSP = g(1, V - {1}) = Min2<=j<=N{C1j + g(j, V - {1, j})}
 g(i, S) = Minjú`S{Cij + g(j, S - {j})}
g(i,úr) = Ci1, i = 2, 3,..., N
g(i, S) = Minjú`S{Cij + g(j, S - {j})}
g(i,úr) = Ci1, i = 2, 3,..., N
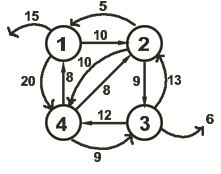
Example:
- g(2,úr) = 5
g(3,úr) = 6
g(4,úr) = 8
- g(2, {3}) = C23 + g(3,úr) = 9 + 6 = 15
g(2, {4}) = C24 + g(4,úr) = 10 + 8 = 18
g(3, {2}) = 13 + 5 = 18
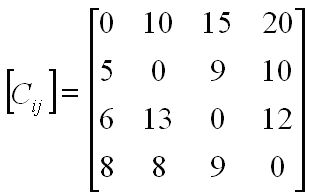 g(3, {4}) = 12 + 8 = 20
g(4, {2}) = 8 + 5 = 13
g(4, {3}) = 9 + 6 = 15
g(3, {4}) = 12 + 8 = 20
g(4, {2}) = 8 + 5 = 13
g(4, {3}) = 9 + 6 = 15
- g(2, {3, 4}) = Min{C23 + g(3, {4}), C24 + g(4, {3})}
= Min{9 + 20, 10 + 25} = 25
g(3, {2, 4}) = Min{C32 + g(2, {4}), C34 + g(4, {2})} = 25
= Min{13 + 18, 12 + 13} = 25
g(4, {2, 3}) = Min{C42 + g(2, {3}), C43 + g(3, {2})} = 23
= Min{8 + 15, 9 + 18} = 23
- g(1, {2, 3, 4}) = Min{C12 + g(2, {3, 4}), C13 + g(3, {2, 4}), C14 + g(4, {2, 3})}
= Min{10 + 25, 15 + 25, 20 + 23} = 35
=> TSP = C12 + C24 + C43 + C31 = 10 + 10 + 9 + 6 = 35
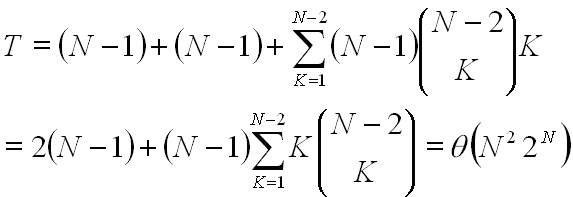






 g(i, S) = Minjú`S{Cij + g(j, S - {j})}
g(i,úr) = Ci1, i = 2, 3,..., N
g(i, S) = Minjú`S{Cij + g(j, S - {j})}
g(i,úr) = Ci1, i = 2, 3,..., N
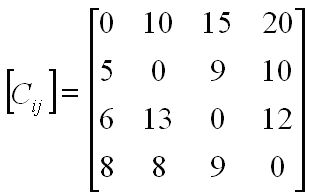 g(3, {4}) = 12 + 8 = 20
g(4, {2}) = 8 + 5 = 13
g(4, {3}) = 9 + 6 = 15
g(3, {4}) = 12 + 8 = 20
g(4, {2}) = 8 + 5 = 13
g(4, {3}) = 9 + 6 = 15