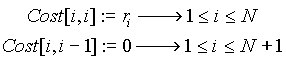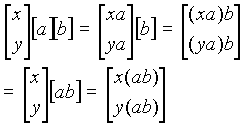
Dynamic Programming
solve a problem by solving all possible sub-problems. Knapsack problems matrix chain product optimal binary search tree 1.Knapsack Problem N = 5 # of itemsM = 17 total capacity
| Name |
A |
B |
C |
D |
E |
|
|
Size |
3 |
4 |
7 |
8 |
9 |
|
|
Value |
4 |
5 |
10 |
11 |
13 |
|
Exmp:
5A --> value = 20
D + E --> value = 24
Program
Cost[i] = highest value for capacity i
best[i] = last item added
| For |
j = 1 to N (use first j items only) |
||
|
|
for |
i = 1 to M (compute each capacity I) |
|
|
|
|
t := Cost [ i - size[j] ] + val [j] |
|
|
|
|
If t > Cost[i] then |
|
|
|
|
|
Cost [I] := t; |
|
|
|
|
Best [I] := j; |
*(on above program, "
Cost [ i - size[j] ]" isbest for rest of Knapsack,"val[j]" means that last item is j)
Illustration :
| 1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
|
|
0 |
0 |
4 |
4 |
4 |
8 |
8 |
8 |
12 |
12 |
12 |
16 |
16 |
16 |
20 |
20 |
20 |
A only |
|
|
|
A |
A |
A |
A |
A |
A |
A |
A |
A |
A |
A |
A |
A |
A |
A |
|
|
0 |
0 |
4 |
5 |
5 |
8 |
9 |
10 |
12 |
13 |
14 |
16 |
17 |
18 |
20 |
21 |
22 |
A,B only |
|
|
|
A |
B |
B |
A |
B |
B |
A |
B |
B |
A |
B |
B |
A |
B |
B |
|
|
0 |
0 |
4 |
5 |
5 |
8 |
10 |
10 |
12 |
14 |
15 |
16 |
18 |
20 |
20 |
22 |
24 |
ABC only |
|
|
|
A |
B |
B |
A |
C |
B |
A |
C |
C |
A |
C |
C |
A |
C |
C |
|
|
0 |
0 |
4 |
5 |
5 |
8 |
10 |
11 |
12 |
14 |
15 |
16 |
18 |
20 |
21 |
22 |
24 |
ABCD only |
|
|
|
A |
B |
B |
A |
C |
D |
A |
B |
B |
A |
C |
C |
D |
C |
C |
|
|
0 |
0 |
4 |
5 |
5 |
8 |
10 |
11 |
13 |
14 |
15 |
17 |
18 |
20 |
21 |
23 |
24 |
ABCDE only |
|
|
|
A |
B |
B |
A |
C |
D |
E |
C |
C |
E |
C |
C |
D |
E |
C |
Best choice: C + C + A for M = 17 value = 24
2.Matrix Chain Product pqr "*" for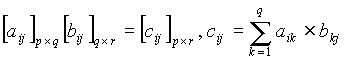
Associating Rules.
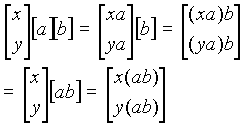
Want to minimize total # "*" among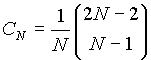 
ways for 
(catalan #: 
)
|
|
|
? |
|
|
|
|
|
Program
Cost[l,r] := min cost for
|
for |
 |
|
|
for |
 |
|
|
|
||
|
|
||
In particular:
|
|
3.Optimal Binary Search Tree
Weighted Internal Path Length (WIPL)
WIPL = 4*2 + 2*3 + 1*1 + 3*3 + 5*4 + 2*2 + 1*3 = 51
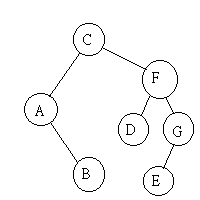
WIPL = 3*1 + (2+2)*2 + (4+1+5+1)*3 = 44
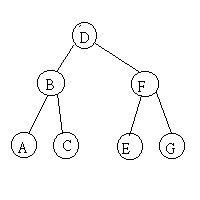
Goal:
Given keys: K1<K2<?<Kn
Frequency: r1 r2 ? rn
Arrange keys in Binary Search Tree to minimize WIPL
Remark:
(1)# binary tree with N node
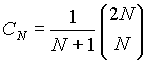
(2)Huffman coding: no need to maintain key order
Algorithm (similar to matrix *)
Minimize
,which 
is root
|
for |
|
|||
|
for |
|
|||
|
|
||||
|
|
||||
|
|
||||
Initialy,
