(defrule example-2
(x)
(y)
(z)
=>)
(defrule example-3
(x)
(y)
=>)
Demo
For Jess, the view command can be used to examine the rete network:
(load-package jess.ViewFunctions)
(view)
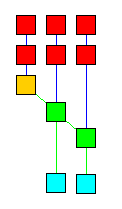
red: Node1 nodes green: Node2 nodes yellow: NodeNot2 nodes blue: Defrule nodes
(defrule Sharing-1
(match ?x red)
(data ~green ?x)
(data ?x ?x)
(other ?z)
=>)
(defrule Sharing-2
(match ?y red)
(data ~green ?y)
(data ?y ?y)
(other ?y)
=>)
(watch activations)
(deffacts information
(match a c e g)
(item a)
(item b)
(item c)
(item d)
(item e)
(item f)
(item g))
(defrule match-1
(match ?x ?y ?z ?w)
(item ?x)
(item ?y)
(item ?z)
(item ?w)
=>
(assert (found-match ?x ?y ?z ?w)))
(defrule match-2
(item ?x)
(item ?y)
(item ?z)
(item ?w)
(match ?x ?y ?z ?w)
=>
(assert (found-match ?x ?y ?z ?w)))
match-1 has 5 partial matches, while match-2 has 2801 partial matches.
Demo:
(defrule match-3
(find-match ?x ?y)
(item ?x)
(item ?y)
=>
(assert (found-match ?x ?y)))
(assert
(find-match a b)
(find-match c d)
(find-match e f)
(item a)
(item b)
(item c)
(item f) )
(matches match-3)
(defrule match-1-pm-1
"Partial matches for pattern 1"
(match ?x ?y ?z ?w)
=>)
(defrule match-1-pm-1-to-2
"Partial matches for patterns 1 to 2"
(match ?x ?y ?z ?w)
(item ?x)
=>)
(defrule match-1-pm-1-to-3
"Partial matches for patterns 1 to 3"
(match ?x ?y ?z ?w)
(item ?x)
(item ?y)
=>)
(defrule match-1-pm-1-to-4
"Partial matches for patterns 1 to 4"
(match ?x ?y ?z ?w)
(item ?x)
(item ?y)
(item ?z)
=>)
(defrule match-1
"Activations for the match rule"
(match ?x ?y ?z ?w)
(item ?x)
(item ?y)
(item ?z)
(item ?w)
=>
(assert (found-match ?x ?y ?z ?w)))
(watch activations)
(watch facts)
Demo:
(defrule produce-twoplets ; useful but too expensive
(list (items $?b $?m $?e))
=>
(assert (front ?b))
(assert (middle ?m))
(assert (back ?e)) )
(assert (list (items a 4 z 2)))
(defrule three-distinct-points
?point1 <- (point (x ?x1)(y ?y1))
?point2 <- (point (x ?x2)(y ?y2))
(test (neq ?point1 ?point2))
?point3 <- (point (x ?x3)(y ?y3))
(test (and (neq ?point2 ?point3))
(neq ?point1 ?point3)))
=>
(assert (distinct-points (x1 ?x1)(y1 ?y1)
(x2 ?x2)(y2 ?y2)
(x3 ?x3)(y3 ?y3))))
(defrule points-share-common-x-or-y-value
(point (x ?x1)(y ?y1))
(point (x ?x2)(y ?y2&:(or (= ?x1 ?x2)
(= ?y1 ?y2))))
=>
(assert (common-x-or-y-value (x1 ?x1)(y1 ?y1)
(x2 ?x2)(y2 ?y2))))
(defrule primary-color
(color ?x&red|green|blue)
=>
(assert (primary-color ?x)))
(deftemplate direction
(slot which-way)
(slot delta-x)
(slot delta-y))
(deffacts direction-information
(direction (which-way north)
(delta-x 0) (delta-y 1))
(direction (which-way south)
(delta-x 0) (delta-y -1))
(direction (which-way east)
(delta-x 1) (delta-y 0))
(direction (which-way west)
(delta-x -1) (delta-y 0)))
(defrule move-direction
(move ?dir)
(direction (which-way ?dir)
(delta-x ?dx) (delta-y ?dy))
?old-location <- (location (x ?old-x) (y ?old-y))
=>
(modify ?old-location (x (+ ?old-x ?dx))
(y (+ ?old-y ?dy))))
(defrule largest-number
(number ?number1)
(not (number ?number2&:(> ?number2 ?number1)))
=>
(printout t "Largest number is " ?number1 crlf))
Let N be the number of facts with the number relation. The time to get the largest number is propotional to the square of N.
A set of rules to reduce the number of comparisons by keeping track of the largest number:
(defrule try-number
(number ?n)
=>
(assert (try-number ?n)))
(defrule largest-unknown
?attempt <- (try-number ?n)
(not (largest ?))
=>
(retract ?attempt)
(assert (largest ?n)))
(defrule largest-smaller
?old-largest <- (largest ?n1)
?attempt <- (try-number ?n2&:(> ?n2 ?n1))
=>
(retract ?old-largest ?attempt)
(assert (largest ?n2)))
(defrule largest-bigger
(largest ?n1)
?attempt <- (try-number ?n2&:(<= ?n2 ?n1))
=>
(retract ?attempt))
(defrule print-largest
(declare (salience -1))
(largest ?n)
=>
(printout t "Largest number is " ?n crlf))
The time to get the largest number using this set of rules is propotional to N.
Previous Modular Design and Execution Control Up TOC Next Procedural Programming