這篇文章想要討論一個物理問題, 雙木塊耦合震盪問題(Coupled Oscillator),想要了解這個問題,需要用常微分方程(Ordinary Differential Equation, ODE)、普通物理、複變,線性代數。
我會從一個有趣的脈絡來切入這個問題,用線性代數中的「Decoupling (解耦)」的概念來解這個問題,也會用Python程式語言來模擬物理現象,希望透過這個問題讓大家了解線性代數理論的巧妙。
- 以下是雙彈簧耦合震動問題的意示圖
單木塊彈簧問題
求解雙木塊耦合震盪問題(Coupled
Oscillator)之前,我們先從比較簡單的單木塊彈簧問題下手,由從虎克定律(Hooke's
Law)木塊的受力在彈性限度範圍內,受到的力與彈簧的形變成線性關係,再根據牛頓第二運動
其中
微分方程式
木塊受力會與木塊與靜力平衡點的位移成負號的關係,且距離越遠(
大),受到的反方向的力也越大。
- 單木塊彈簧問題意示圖
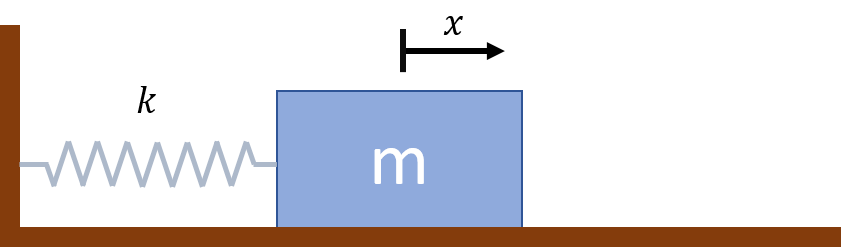
為了呼應後面的我們的討論,我們令
回想最簡單的ODE,
想要求解
將
滿足以上等式有兩個可能,
由於上述原因,我們考慮一般的狀況,也就是當
且
因為
注意,指數的虛數次方是透過 Euler Formula
在ODE裡面有個重要的定理,叫做重疊定理(Superposition Theorem):
對於齊次的常微分方程(ODE),所有解都可以透過線性獨立解的線性組合所生成。
重疊定理的證明不困難,我們可以簡易說明如下:
齊次ODE的解集合實際上就是一個subspace,因為子空間的定義,子空間中的線性獨立向量的線性組合,還會落在該子空間中。用線性代數的語言來說,齊次ODE解集合的是一個kernel space,kernel space也是線性變換四個基本子空間中的一個。
透過重疊原理,如果我們找出方程式
又因為
「實條件」(Realily):如果一個複數
其中
由比較係數得到,
根據「實條件」,我們得到式
用Euler Formula 且假設
令
將位移函數對時間
因為有
所以只要給定木塊的初始位置
我們用 Python 程式語言模擬單木塊彈簧的動畫,用到的套件為 Vpython 與 Numpy
給定初始參數為
彈簧模擬動畫與 x-t 圖曲線

程式碼如下: 程式的主要邏輯是用推導出來的解
# coding=utf-8
from vpython import *
import numpy as np
"""
1. 參數設定, 設定變數及初始值
"""
size = 0.1 # 木塊邊長
L = 1 # 地板長度
k = 3
m = 1
x0 = 0
x0_dot = 0.3
t = 0 # 時間
T = 30
dt = 0.01 # 時間間隔
"""
2. 畫面設定
"""
scene = canvas(title=f"單木塊彈簧,假設地版無摩擦 m={m}, k={k}", width=800, height=300, x=0, y=0, center=vec(0, 0.1, 0), background=vec(0, 0.6, 0.6))
floor = box(pos=vec(0, 0, 0), size=vec(L, 0.1*size, 0.5*L), color=color.blue)
wall1 = box(pos=vec(-L/2, 0.3*L/2, 0), size=vec(0.1*size, 0.3*L, 0.5*L), color=color.blue)
cube1 = box(pos=vec(x0, 0.55*size, 0), size=vec(size, size, size), color=color.red, v=vec(0, 0, 0))
spring1 = helix(pos=vec(-L/2, 0.55*size, 0), radius=0.3*size, thickness=0.05*size, color=color.yellow)
spring1.axis = cube1.pos - spring1.pos - vec(size/2, 0, 0)
gd = graph(title="x-t plot", width=600, height=450, x=0, y=600, xtitle="t(s)", ytitle="x(m)", label="cos(x)")
gd2 = graph(title="v-t plot", width=600, height=450, x=0, y=1050, xtitle="t(s)", ytitle="v(m/s)")
xt = gcurve(graph=gd, color=color.red)
vt = gcurve(graph=gd2, color=color.red)
"""
3. 物體運動部分, 木塊到達地板邊緣時停止執行
"""
while(t<T):
rate(100)
cube1.pos.x = - 0.2*L + x0*(np.cos(np.sqrt(k/m)*t)) \
+ (x0_dot/np.sqrt(k/m))*np.sin(np.sqrt(k/m)*t)
cube1.v.x = -x0*(np.sqrt(k/m))*np.sin(np.sqrt(k/m)*t) \
+ x0_dot*np.cos(np.sqrt(k/m)*t)
spring1.axis = cube1.pos - spring1.pos - vec(size/2, 0, 0)
xt.plot(pos=(t, cube1.pos.x))
vt.plot(pos=(t, cube1.v.x))
t += dt
print("Done")雙木塊耦合震盪問題(Coupled Oscillator)
我們有兩個質量為m的木塊,有兩面固定不動的牆,木塊之間,木塊與牆壁之間用彈性係數為
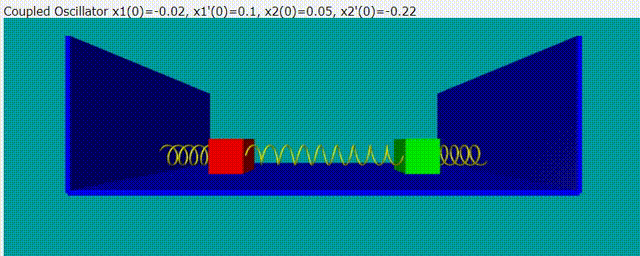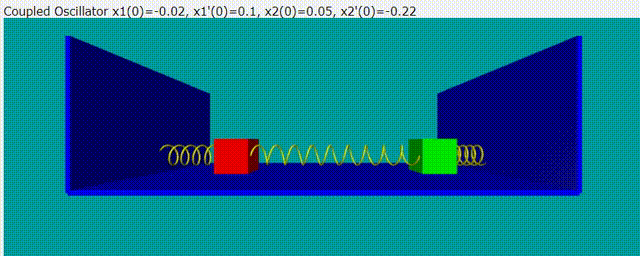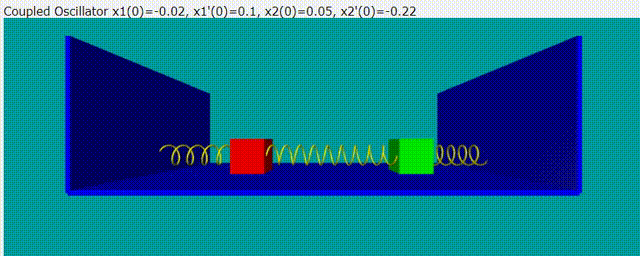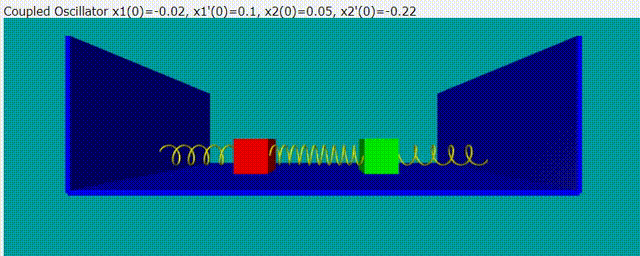
雙木塊耦合震盪問題的意示圖如下圖:
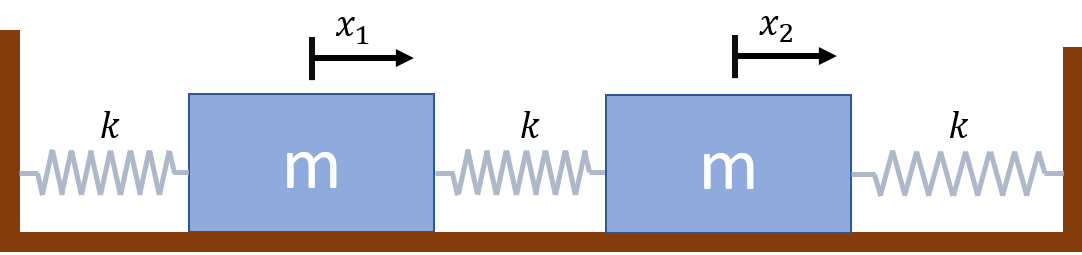
因為虎克定律(Hooke's Law),木塊的受力在彈性限度範圍內,受到的力與彈簧的形變成線性關係,假設向右的力量為正。
假設「左」邊的木塊往右位移了
假設兩個木塊分別向右移動

在以上的意示圖中,兩個木塊位移的關係式為
觀察「左」木塊:
對於「左」木塊的左邊的彈簧,也就是被拉伸了
的位移,根據Hooke's Law 會產生向左 的力量,因為向左所以記做 對於「左」木塊的右邊的彈簧(整個系統中間的彈簧),可以考慮以下幾個情況
如果
,也就是把「右」木塊當作一個不動的牆壁,受力為 。 如果
,對於「左」木塊的右邊彈簧,彈簧沒有形變,根據Hooke's Law 不會產生力。 如果
,對於「左」木塊的右邊彈簧,彈簧被壓縮了,根據Hooke's Law 會產生將「左」木塊往「左」的力量,力量大小為 ,考慮向右為正,記做 。 如果
,對於「左」木塊的右邊彈簧,彈簧被拉伸了,根據Hooke's Law 會產生將「左」木塊往「右」的力量,力量大小為 ,考慮向右為正,記做 。 總和以上討論
「左」木塊受的力量總合為
,根據牛頓第二運動定律
- 觀察「右」木塊:
與「左」木塊的討論類似,不過整個系統中間的彈簧受力的方向與「左」木塊的情況相反,這裡留給讀者自己推導
「右」木塊受的力量總合為
,根據牛頓第二運動定律
雙木塊耦合震盪問題,可以寫成二階齊次ODE方程組:
1. 透過變數變換求解雙木塊耦合震盪問題
這裡我們用一個技巧,先把
接著再將
令
式
透過
方程組
但是我們並不想要解
由
把
再把
Coupled Oscillator 的解可以寫成:
速度,也就是位移函數的微分,透過
觀察解
- 當
:
Coupled Oscillator的解
簡化為
- 當
:
Coupled Oscillator的解
簡化為
解
同樣的,我們用 Python 程式語言模擬單木塊彈簧的動畫
Normal Mode 1: 頻率為
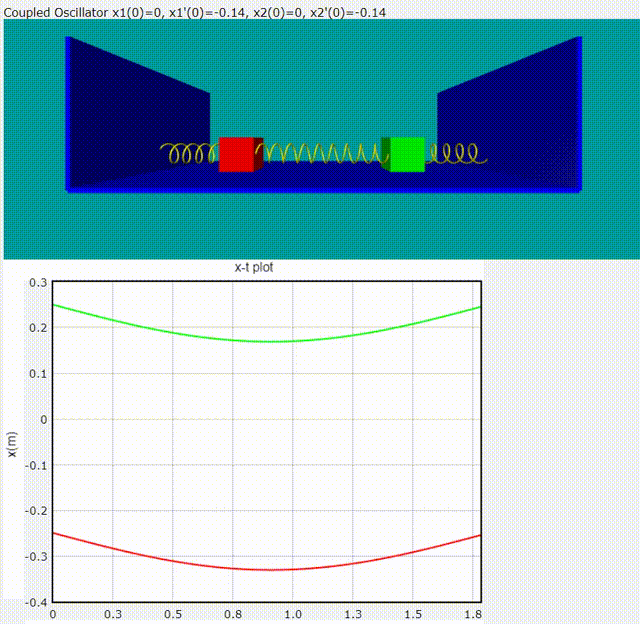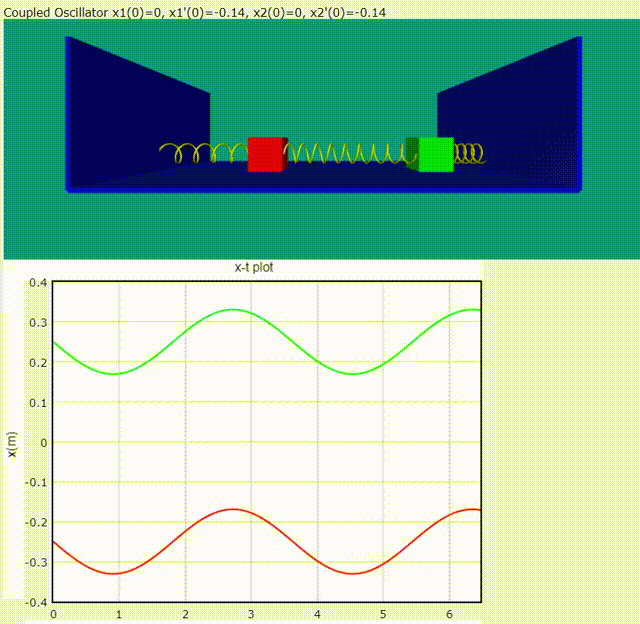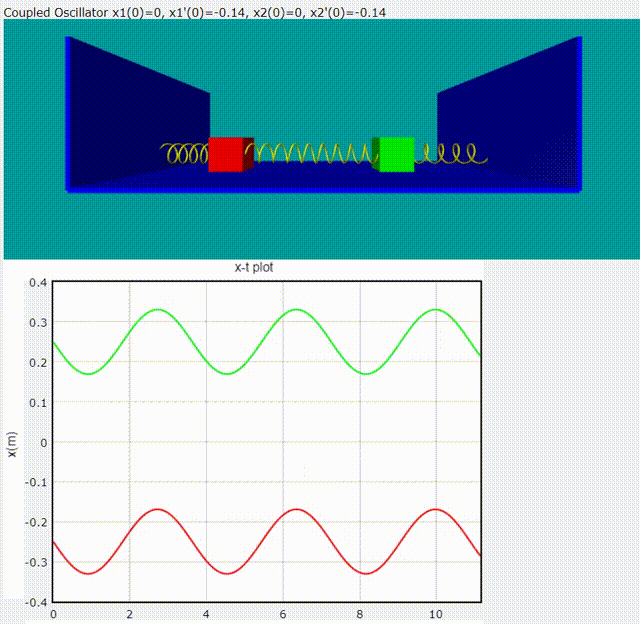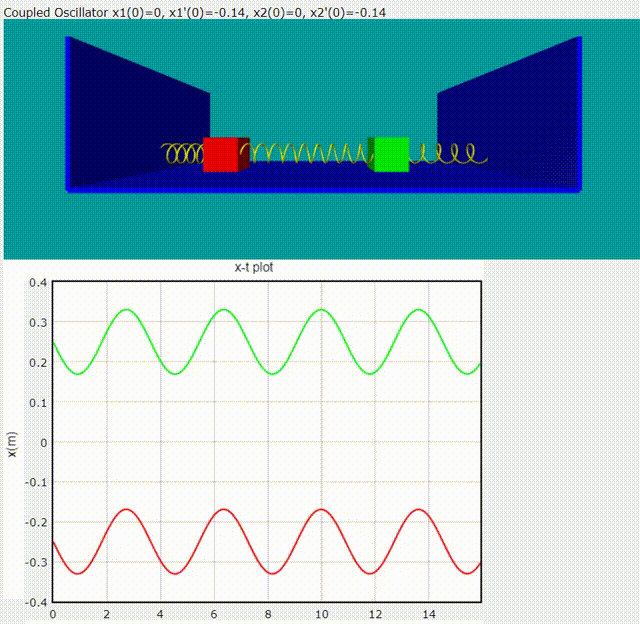
Normal Mode 2: 頻率為
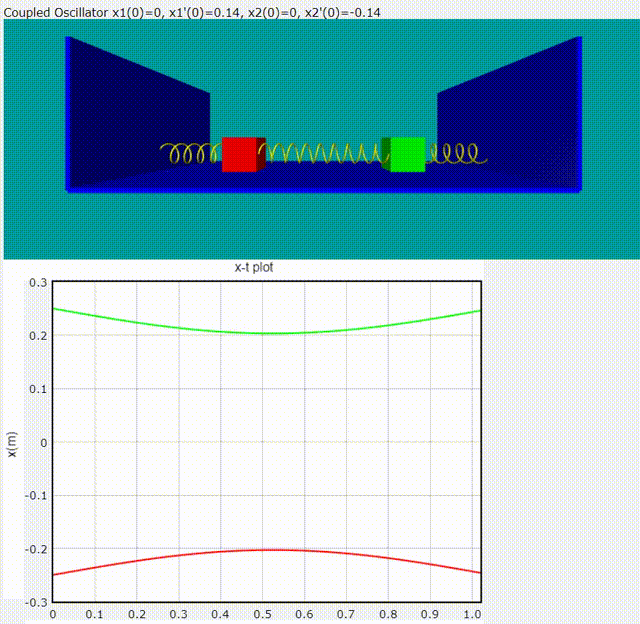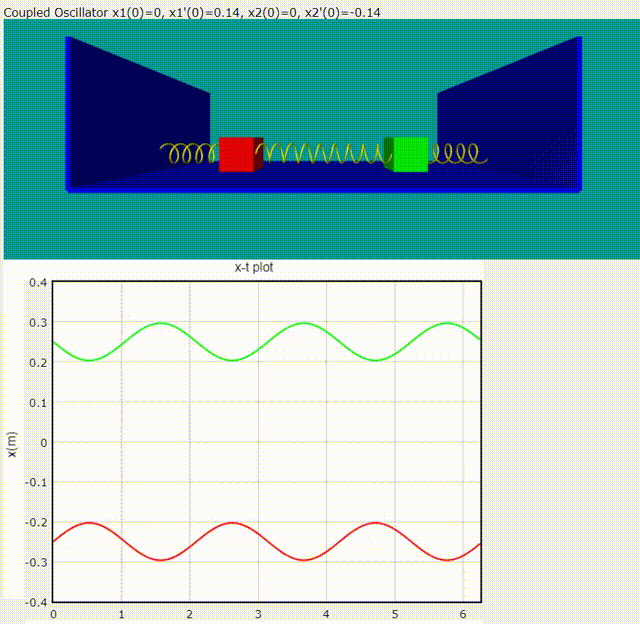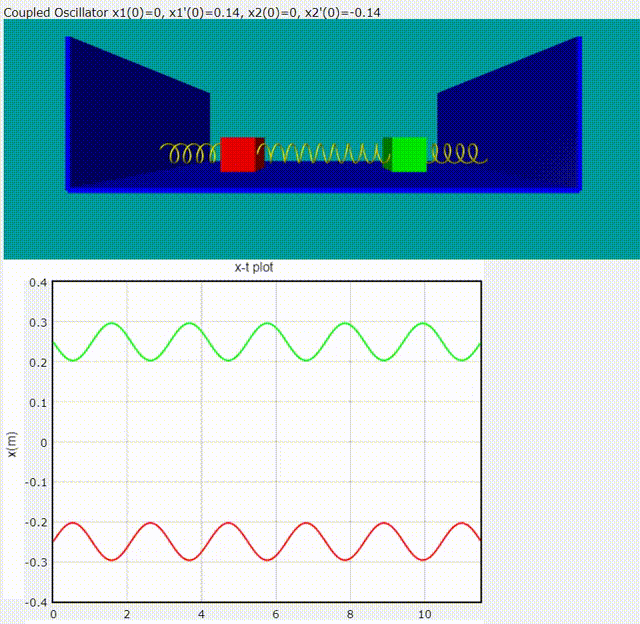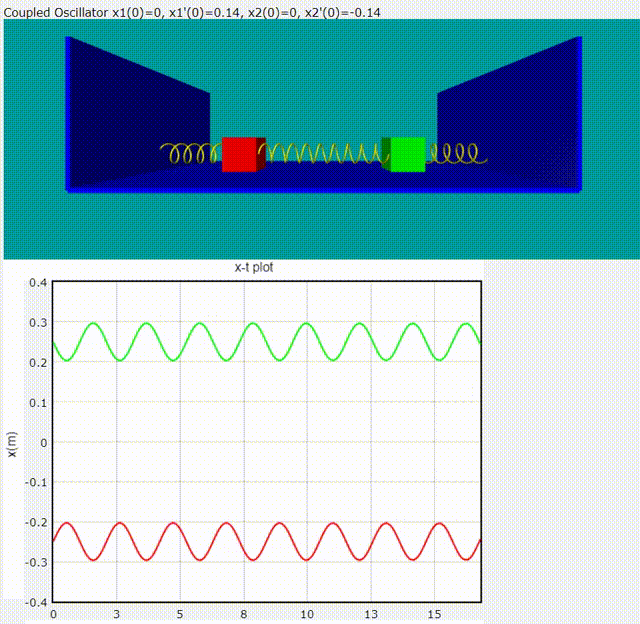
給定隨意的初始條件,雙木塊耦合震盪模擬動畫
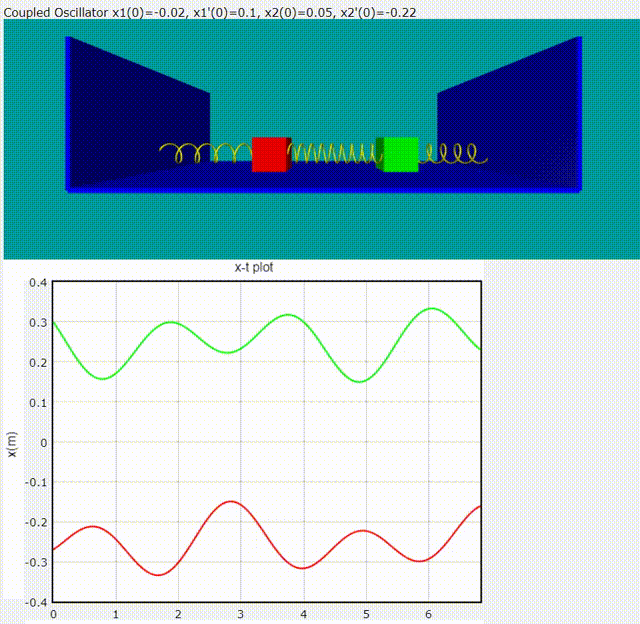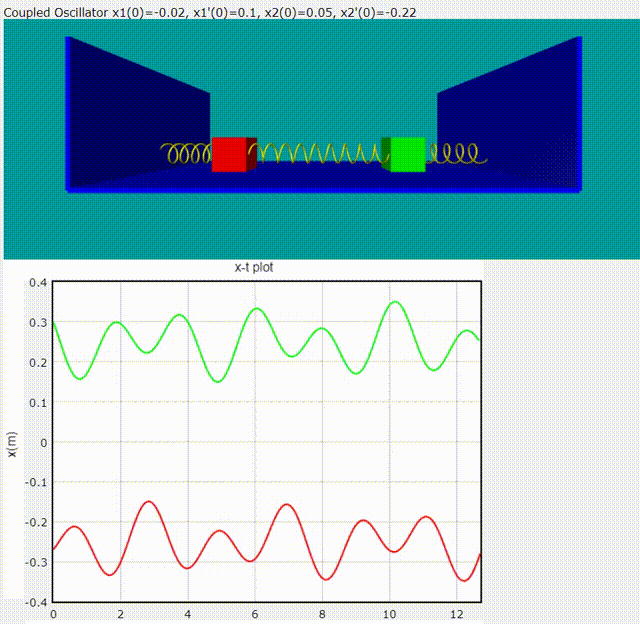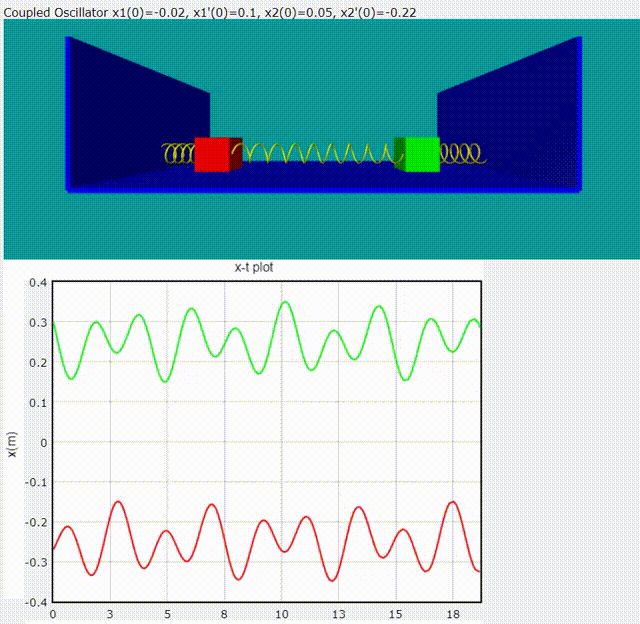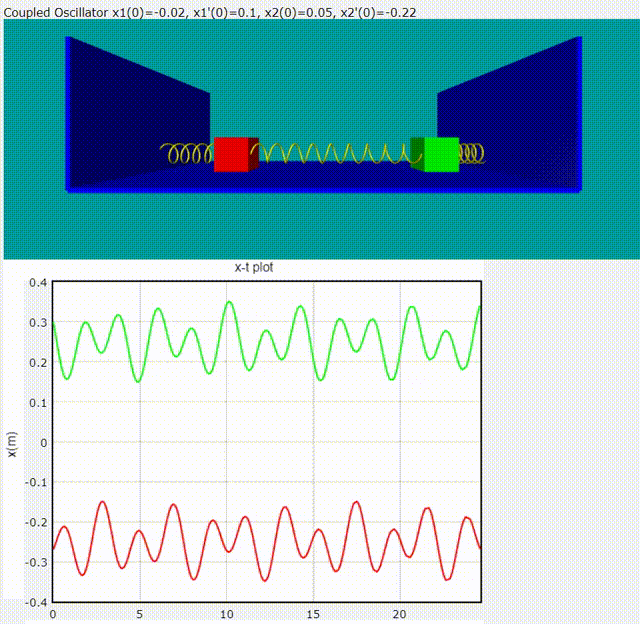
程式碼如下:
# coding=utf-8
from vpython import *
import numpy as np
"""
1. 參數設定, 設定變數及初始值
"""
size = 0.1 # 木塊邊長
L = 1 # 地板長度
k = 3
m = 1
# Normal Mode for frequency = k/m
# x10 = 0
# x10_dot = -0.14
# x20 = 0
# x20_dot = -0.14
# Normal Mode for frequency = 3k/m
# x10 = 0
# x10_dot = 0.14
# x20 = 0
# x20_dot = -0.14
#Coupled Oscillator
x10 = -0.02
x10_dot = 0.10
x20 = 0.05
x20_dot = -0.22
t = 0 # 時間
T = 30
dt = 0.01 # 時間間隔
"""
2. 畫面設定
"""
scene = canvas(title=f"Coupled Oscillator x1(0)={x10}, x1'(0)={x10_dot}, x2(0)={x20}, x2'(0)={x20_dot}", width=800, height=300, x=0, y=0, center=vec(0, 0.1, 0), background=vec(0, 0.6, 0.6))
floor = box(pos=vec(0, 0, 0), size=vec(L, 0.1*size, 0.5*L), color=color.blue)
wall1 = box(pos=vec(-L/2, 0.3*L/2, 0), size=vec(0.1*size, 0.3*L, 0.5*L), color=color.blue)
wall2 = box(pos=vec(L/2, 0.3*L/2, 0), size=vec(0.1*size, 0.3*L, 0.5*L), color=color.blue)
cube1 = box(pos=vec(x10, 0.55*size, 0), size=vec(size, size, size), color=color.red, v=vec(0, 0, 0))
cube2 = box(pos=vec(x20, 0.55*size, 0), size=vec(size, size, size), color=color.green, v=vec(0, 0, 0))
spring1 = helix(pos=vec(-L/2, 0.55*size, 0), radius=0.3*size, thickness=0.05*size, color=color.yellow)
spring1.axis = cube1.pos - spring1.pos - vec(size/2, 0, 0)
spring2 = helix(pos=vec(x10, 0, 0), radius=0.3*size, thickness=0.05*size, coils=9, color=color.yellow)
spring2.pos = cube1.pos + vec(size/2, 0, 0)
spring2.axis = cube2.pos - cube1.pos - vec(size, 0, 0)
spring3 = helix(pos=cube2.pos + vec(size/2, 0, 0), radius=0.3*size, thickness=0.05*size, color=color.yellow)
spring3.axis = vec(L/2, 0.55*size, 0) - cube2.pos - vec(size/2, 0, 0)
gd = graph(title="x-t plot", width=600, height=450, x=0, y=600, xtitle="t(s)", ytitle="x(m)")
gd2 = graph(title="v-t plot", width=600, height=450, x=0, y=1050, xtitle="t(s)", ytitle="v(m/s)")
xt = gcurve(graph=gd, color=color.red)
vt = gcurve(graph=gd2, color=color.red)
xt2 = gcurve(graph=gd, color=color.green)
vt2 = gcurve(graph=gd2, color=color.green)
"""
3. 物體運動部分, 木塊到達地板邊緣時停止執行
"""
while(t<T):
rate(100)
cube1.pos.x = - 0.25*L + 0.5*((x10+x20)*np.cos(np.sqrt(k/m)*t) \
+ (x10_dot+x20_dot)/np.sqrt(k/m)*np.sin(np.sqrt(k/m)*t) \
+ (x10-x20)*np.cos(np.sqrt(3*k/m)*t) \
+ (x10_dot-x20_dot)/np.sqrt(3*k/m)*np.sin(np.sqrt(3*k/m)*t))
cube2.pos.x = 0.25*L + 0.5*((x10+x20)*np.cos(np.sqrt(k/m)*t) \
+ (x10_dot+x20_dot)/np.sqrt(k/m)*np.sin(np.sqrt(k/m)*t) \
- (x10-x20)*np.cos(np.sqrt(3*k/m)*t) \
- (x10_dot-x20_dot)/np.sqrt(3*k/m)*np.sin(np.sqrt(3*k/m)*t))
cube1.v.x = 0.5*((np.sqrt(k/m)*(-(x10+x20)*np.sin(np.sqrt(k/m)*t) \
+(x10_dot+x20_dot)/np.sqrt(k/m)*np.cos(np.sqrt(k/m)*t))) \
+(np.sqrt(3*k/m))*((x20-x10)*np.sin(np.sqrt(3*k/m)*t) \
+(x10_dot-x20_dot)/np.sqrt(3*k/m)*np.cos(np.sqrt(3*k/m)*t)))
cube2.v.x = 0.5*((np.sqrt(k/m)*(-(x10+x20)*np.sin(np.sqrt(k/m)*t) \
+(x10_dot+x20_dot)/np.sqrt(k/m)*np.cos(np.sqrt(k/m)*t))) \
-(np.sqrt(3*k/m))*((x20-x10)*np.sin(np.sqrt(3*k/m)*t) \
+(x10_dot-x20_dot)/np.sqrt(3*k/m)*np.cos(np.sqrt(3*k/m)*t)))
spring1.axis = cube1.pos - spring1.pos - vec(size/2, 0, 0)
spring2.pos = cube1.pos + vec(size/2, 0, 0)
spring2.axis = cube2.pos - cube1.pos - vec(size, 0, 0)
spring3.pos = cube2.pos + vec(size/2, 0, 0)
spring3.axis = vec(L/2, 0.55*size, 0) - cube2.pos - vec(size/2, 0, 0)
xt.plot(pos=(t, cube1.pos.x))
vt.plot(pos=(t, cube1.v.x))
xt2.plot(pos=(t, cube2.pos.x))
vt2.plot(pos=(t, cube2.v.x))
t += dt
print("Done")2. 解耦 (Deoupling)與線性代數中 Eigenvalue, Eigenvector的關係
變數變換法巧妙的利用式
變數變換前原本「Coupled」在一起的二階齊次ODE
這裡「Coupled」的意思是,變數不只與自己相關,還與其他變數相關,舉例來說
如何找到
以下我們講述這個變數變換與Eigenvalue,Eigenvector理論的關係。
首先,令
回想特徵值(Eigenvalue)與特徵向量(Eigenvector)的關係:
如果我們有矩陣方程
,此時稱 為 矩陣的Eigenvector,且對應的Eigenvalue為
對於矩陣
注意:為了要與前面變數變換
求解矩陣
現在我們驗證這兩組Eigenvalue與Eigenvector
因為Eigenvector
其中
將
總結
因為
等式左右相等,也就是對應的基底
到這裡我們終於知道為什麼
我們要假設 ,原因就是要與線性代數中的Eigenvalue的符號互相呼應!!
由單木塊彈簧問題的解
將
將
得到
現在我們將
最後再將
最後我們做一個結論,巧妙的變數變換
由
透過基底表示的符號可以記作:
所以解耦 (Deoupling)的意思就將向量表示成矩陣
所以整個求解的思路可以總結如下:
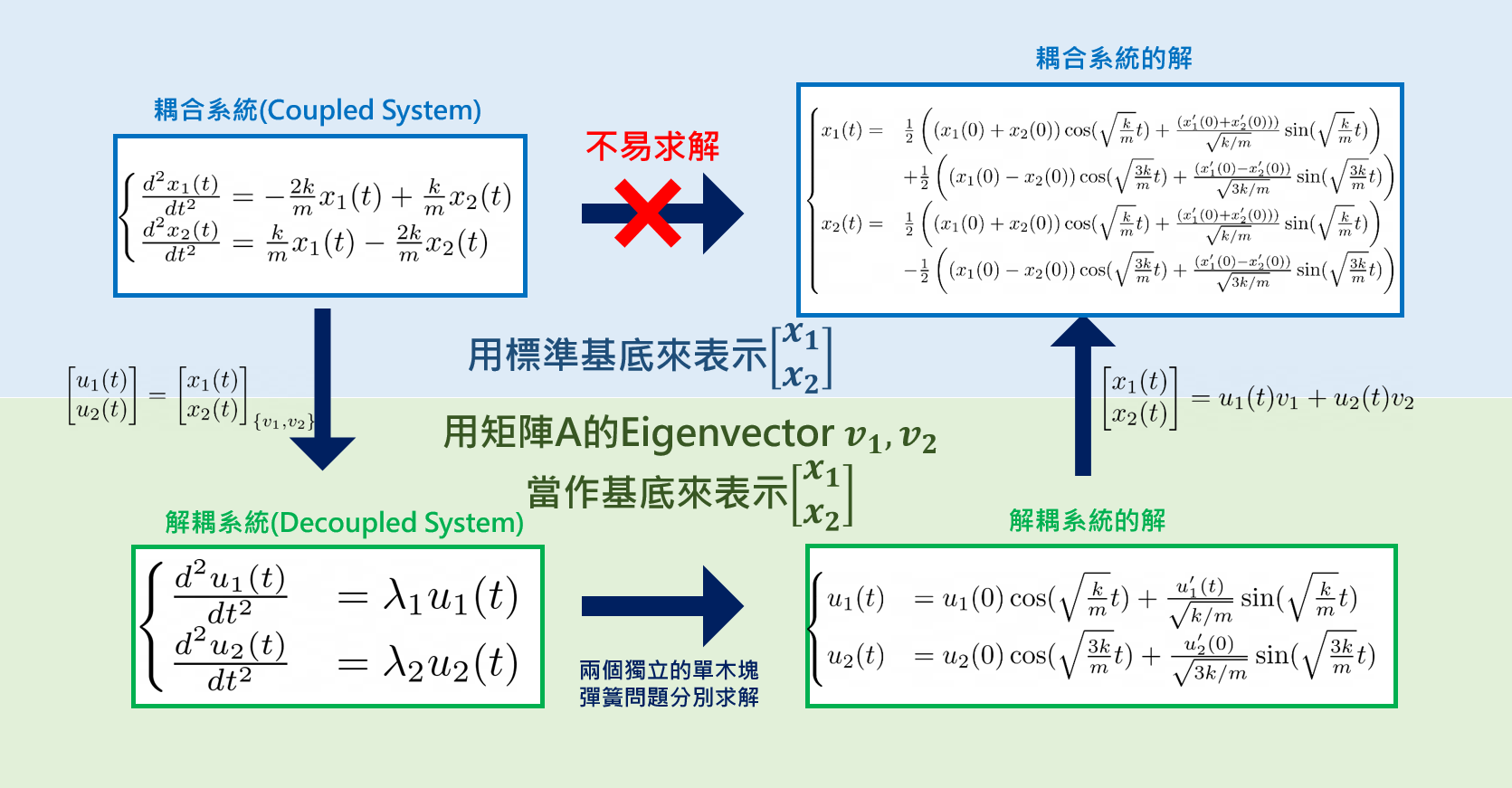
總結一下這篇文章:
- 首先從單木塊彈簧問題開始求解,用Hooke's Law的觀察描述了彈簧受力的微分方程式,再用到物理性質的限制,還有複變的Euler Formula,求得了單木塊彈簧問題的解
- 接著開始考慮我們的目標雙木塊耦合震盪問題。透過一個特殊的變數變換
- 最後我們用線性代數的理論基礎,Eigenvalue與Eigenvector來說明解耦 (Deoupling)的概念,只要用線性獨立的Eigenvector當作基底來表示將想求解的問題,問題可以被解耦 (Deoupling),也就對應到(2.)提到的變數變換,所以把整個求解雙木塊耦合震盪問題的思路串起來了。
這個脈絡我覺得很有趣,可以深刻地了解線性代數怎麼應用來解物理問題,我們也特別用程式來模擬木塊運動,讓大家也看出來,Normal Mode 確實是比較簡單的運動模式,兩個木塊不會有多餘的相互影響(Coupled)
Reference
Sadun, L. A. (2007). Applied linear algebra: The decoupling principle. American Mathematical Soc..
