Soft Thresholding 與 L-1 Minimization之間的關係

2022/11/24 數學數學與統計最佳化微積分

考慮一個機器學習、統計中常常會遇到的一個convex optimization問題

(LASSO) 問題 (Least Absolute Shrinkage and Selection Operator)

where

令且

且

問題(1) 可以簡化成

將改寫成

$調整係數$

問題(2) 的constraint 也可以改寫成，然後將問題(2) 改寫成 Lagrange Form

where , and .

我們用問題(3) 當作起點開始推導

根據 norm 定義展開：

其中

也就是說，對於每一個 component 我們可以獨立求解

對每個分量微分：

其中絕對值無法直接微分，所以用subdifferent取代

假設

if 有變數需化簡

以上公式被稱為 Soft Thresholding

又因為這個是convex function，當極值發生時，就是微分=0的解，所以我們推出了這個LASSO 的closed form solution。

現在將與的下標都去掉

以下是以縱坐標為，橫坐標為繪圖

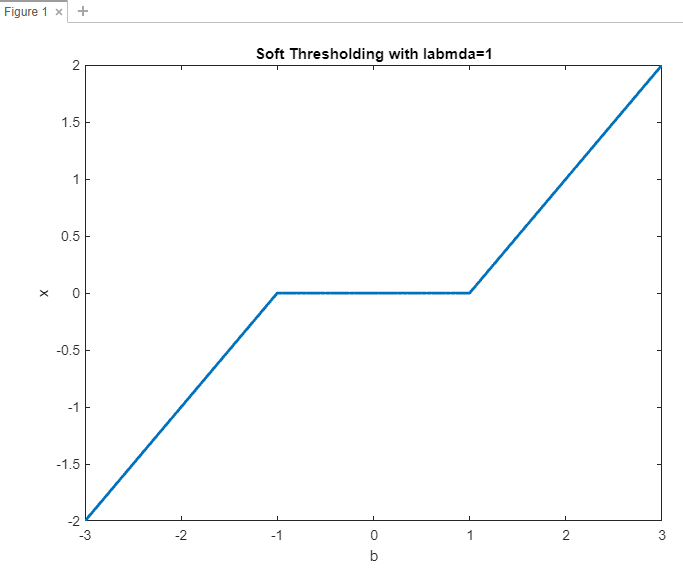
這個圖形水平線的寬度與有關係，在極端的情況下，很大的時候，的解會幾乎都是水平線，也就是說產生的penalty太大，以至於完全無法fitting 。

可以將 (4) 式改寫，將 soft thresholding 看成一個運算子(opeator)，這個運算子就代表著求解問題(3)，取名為，給定與 vector 就可以求解出 LASSO 的解向量。

改寫成

這個運算子計算非常簡單，只需要比較與就能得到，計算複雜度為。

也就是只根求解的向量的長度有關，這個運算子常在各種傳統機器學習，字典學習，影像處理，稀疏表示，基底追蹤等演算法中扮演重要的角色。

對應於【軟】閾值 Soft Thresholding 也有【硬】閾值 Hard Thresholding 這兩個是很類似的主題，之後有空也會在整理一篇。

LOADING...