|
In the advanced section of HCR, we concentrate on: 1. the bended ellipse features,
2. the comparison method used in classification and 3. the process of network training.
Bended ellipse features (J.13)
Remember what features do we extract from "characters" in Introduction?
Yes, they are 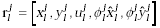 , where , where 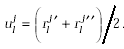 and
and 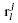 means the lth
feature vector of the jth radical. So the jth radical is represented
as means the lth
feature vector of the jth radical. So the jth radical is represented
as 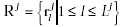 . Similarly, the 1st
handprinted character is represented as . Similarly, the 1st
handprinted character is represented as 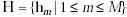 where
where 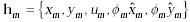 is the mth
feature vector of the handprinted character. For a set of input handprinted characters,
each character in the set can be represented by is the mth
feature vector of the handprinted character. For a set of input handprinted characters,
each character in the set can be represented by 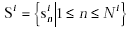 (i means ith handprinted character, and this set of input has total
N of them) and
(i means ith handprinted character, and this set of input has total
N of them) and 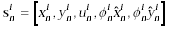 is the nth
feature vector of the ith character. Now we explain the idea of feature
vector in detail. is the nth
feature vector of the ith character. Now we explain the idea of feature
vector in detail.
For characters like " ", each vertex (seed)
has two connecting sides. For such a seed, it has 1 feature vector. For characters
like " ", each vertex (seed)
has two connecting sides. For such a seed, it has 1 feature vector. For characters
like " ", the seed at the center intersection has four
connecting sides; therefore it has 6 feature vectors (left&up, left&right,
left&down, right&up, right&down, up&down). The way to calculate the number of
feature vectors is ", the seed at the center intersection has four
connecting sides; therefore it has 6 feature vectors (left&up, left&right,
left&down, right&up, right&down, up&down). The way to calculate the number of
feature vectors is 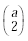 where
a is the number of sides connected to the seed. For each seed, we write all of
its feature vectors in a concept feature to simplify further reference and calculation. where
a is the number of sides connected to the seed. For each seed, we write all of
its feature vectors in a concept feature to simplify further reference and calculation.
Compatibility (J.13)
In the matching process, we compare each handprinted character and standard
character with each radical. For example, for the jth radical Rj,
we calculate its compatibility with handprinted character H and let this
value be 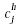 . When all the
radicals are compared with the handprinted character, we get . When all the
radicals are compared with the handprinted character, we get 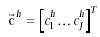 .
And the compatibility of radicals to each standard characters can be writeen as .
And the compatibility of radicals to each standard characters can be writeen as
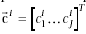 where where 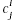 is the compatibility of the jth radical and the ith standard
character. For the recognition task, we would like to minimize the value of
is the compatibility of the jth radical and the ith standard
character. For the recognition task, we would like to minimize the value of 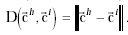 and the "standard character" that achieves this minimum value is the classification
result we want.
and the "standard character" that achieves this minimum value is the classification
result we want.
Next we will explain the inter-feature similarity and inter-link similarity
mentioned in Introduction. Assume we want to compare
the corresponding feature pairs 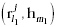 and
and 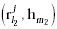 . When feature vectors
l1 and l2 are connected and feature vectors m1 and
m2 are connected (which satisfies inter-link similarity), then . When feature vectors
l1 and l2 are connected and feature vectors m1 and
m2 are connected (which satisfies inter-link similarity), then 
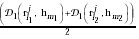 , otherwise set the value
to be -µ. (We set -µ=10). We define D1 to be , otherwise set the value
to be -µ. (We set -µ=10). We define D1 to be  ,
which is the inter-feature similarity. ,
which is the inter-feature similarity.
Train the network (J.13)
In our network, we write every converged state as a matrix V, each row of V
represents the features of a radical and each column represents the features
of a handprinted character. When Vlm=1, it means that the lth
feature of the radical and the mth feature of the handprinted character
have correspondence. We can add this pair 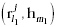 to the route
to the route 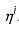 . To ensure
the correctness of the route, V must comply to the following rules: . To ensure
the correctness of the route, V must comply to the following rules:
 | Only one 1 in each row(feature-to-feature can not be 1 to many or many to 1) |
 | At most one 1 in each column |
 | When network converges, the sum of the compatibility of the route should be maximized |
We can write the above restrictions as an function, we call that the energy function:
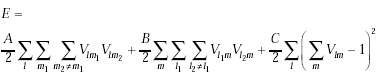 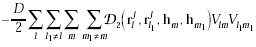
|These three terms
satisfies rule 1 and 2
||
This term satisfies rule 3
|
Where A=500, B=500, C=500/N, D=500N/80 and N=LjM.
The network state changes as the following equation:
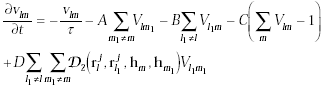 where where 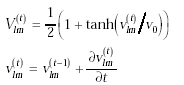
For initial value of Vlm, if 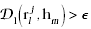 (
(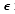 is the threshold), then
we set Vlm=1. is the threshold), then
we set Vlm=1.
Our network uses backpropogation (because simple classification is not enough for Chinese characters),
and the network structure is as follows:
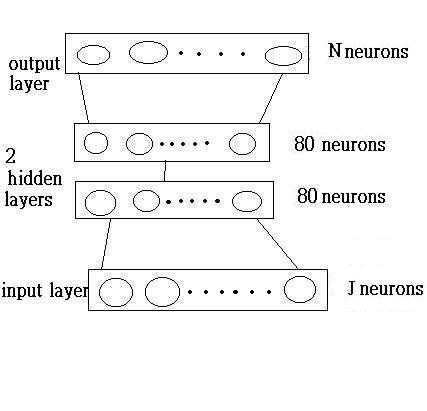
We use the 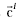 (where 1<=i<=N,
N is the number of standard characters) from above to train the network. Which means
if we input (where 1<=i<=N,
N is the number of standard characters) from above to train the network. Which means
if we input 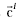 then the first
neuron of the output layer would be on state, and others be off state. When the network
converges, we can use it as the handprinted character classifier. then the first
neuron of the output layer would be on state, and others be off state. When the network
converges, we can use it as the handprinted character classifier.
|