Cohen-Grossberg

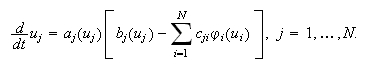
For neural networks obey the following differential equation: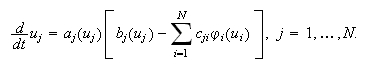

They will admit this energy function: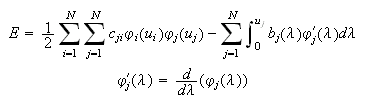

The constrains for the energy function above are

1. symmetric : .

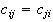2. nonnegativity : .

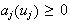3. monotonicity :

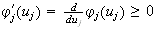
Cohen-Grossberg theorem: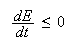

Hairy Network

The neurodynamic equation is:

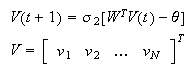
The global energy function for hairy network is:

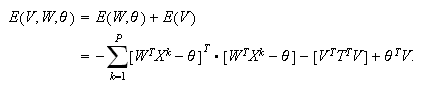
where is a network matrix related to :

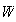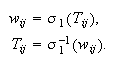
where 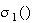and 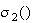are sigmoid functions.

Hopfield

discrete model

The neurodynamic equation is: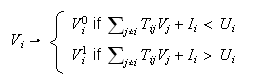

The energy function for Hopfield discrete model is: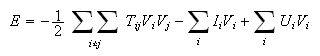

continuous model

The neurodynamic equation is: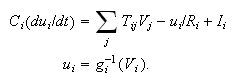

The energy function for Hopfield continuous model is: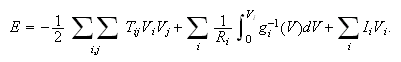

where 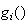is a sigmoid function.

ECR

The global energy function for ECR is:

e-AM

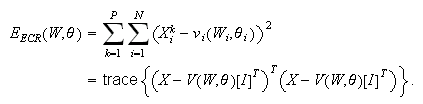
The global energy function for e-AM model is:

temporal AM

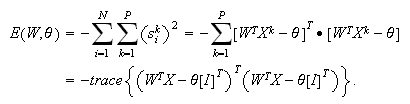
The original temporal AM proposed in (Amari, 1972) is implemented according to Hebb's postulate, which is similar to HM, as follows: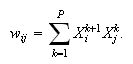The energy function for the temporal model is:

Comparison

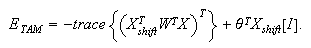
We list the symbol comparison in Table 1 and rewrite all equations of Cohen-Grossberg Theorem, the Hopfield Model and Hairy Network with identical symbols in Table 2,3.

Correspondence between the Cohen-Grossberg Theorem, the Hopfield Netowrk and Hairy Network

Cohen-Grossberg Theorem	discrete HM	continuous HM	Hairy Network

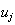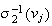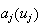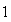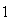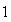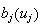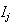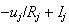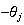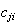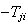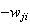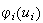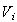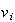Neurodynamic equations with identical symbols

	Neurodynamic equation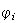
Cohen-Grossberg Theorem		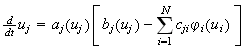sigmoid function
discrete HM		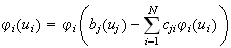unit step function
continuous HM		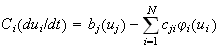sigmoid function
Hairy Network		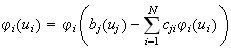sigmoid function

¡@

Energy functions with identical symbols

	Energy function
Cohen-Grossberg Theorem
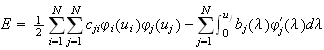discrete HM
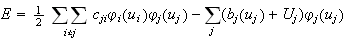continuous HM
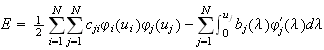Hairy Network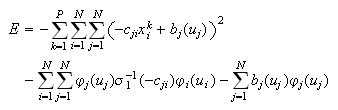